浙江省丽水市2020-2021学年七年级上学期数学期末模拟试卷

试卷更新日期：2021-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 给出四个数1，0，－ $\frac{1}{3}$ ，0.3，其中最小的是（）

A、0 B、1 C、－ $\frac{1}{3}$ D、0.3

查看试题解析
2. 三星堆博物馆于1992年8月奠基，1997年10月建成开放，位于全国重点文物保护单位三星堆遗址东北角，地处广汉城西鸭子河畔，是中国一座现代化的专题性遗址博物馆．小伟在“百度”搜索“三星堆博物馆”，找到相关结果为7360000条，其中7360000用科学记数法表示为（）

A、 $7.36 \times 10^{6}$ B、 $736 \times 10^{4}$ C、 $73.6 \times 10^{5}$ D、 $7.36 \times 10^{7}$

查看试题解析
3. 在3.14， $\sqrt{5}$ ， $\frac{22}{7}$ ，－2这4个数中，属于无理数的是（）

A、3.14 B、 $\sqrt{5}$ C、 $\frac{22}{7}$ D、－2

查看试题解析
4. 下列各式中运算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $4 a - 3 a = 1$ C、 $3 a^{2} b - 2 {ba}^{2} = a^{2} b$ D、 $3 a^{2} + a^{3} = 4 a^{5}$

查看试题解析
5. 方程 $2 x + a = 4$ 的解是 $x = - 2$ ，则 $a =$ （）

A、–8 B、0 C、2 D、8

查看试题解析
6. 某商店的老板销售一种商品，他以不低于进价20%的价格才能出售，但为了获得更多利润，他以高出进价80%的价格标价，若你想买下标价为360元的这种商品，且使商店老板愿出售，你最多可要求老板降价（）

A、80元 B、100元 C、120元 D、160元

查看试题解析
7. 如图，直线 $A B$ ， $C D$ 相交于点O，射线 $O E$ 平分 $∠ A O C$ ，若 $∠ B O D = 68 °$ ，则 $∠ B O E$ 等于（）

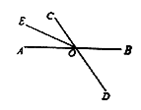A、34° B、112° C、146° D、148°

查看试题解析
8. 若用A、B、C分别表示有理数 $a 、 b 、 c$ ，O为原点如图所示.化简 $| a - c | + | b - a | - | c - a |$ 的结果为（）

A、 $a + 2 b - c$ B、 $b - 3 a + 2 c$ C、 $a + b - 2 c$ D、 $b - a$

查看试题解析
9. 某商品进价为每件a元，商店将价格提高 30% 作零售价销售，在销售旺季过后，商店又以 8 折的价格开展促销活动，这时该商品每件的售价为（）

A、a 元 B、0.8a 元 C、1.04a 元 D、0.92a 元

查看试题解析
10. 日常生活中我们使用的数是十进制数 $.$ 而计算机使用的数是二进制数，即数的进位方法是“逢二进一” $.$ 二进制数只使用数字0，1，如二进制数1101记为 $1101_{2}$ ， $1101_{2}$ 通过式子 $1 \times 2^{3} + 1 \times 2^{2} + 0 \times 2 + 1$ 可以转换为十进制数13，仿照上面的转换方法，将二进制数 $11101_{2}$ 转换为十进制数是（）

A、4 B、25 C、29 D、33

查看试题解析

二、填空题

11. 若4x⁴yⁿ与﹣5x^my²的和仍为单项式，则m+n＝．

查看试题解析
12. 若∠α＝25°42′，则它余角的度数是.

查看试题解析
13. $\sqrt{{(- 2)}^{2}}$ 的平方根是； $8 a^{3}$ 的立方根是 .

查看试题解析
14. 铁一中分校下午放学时间是5：45，此时时针与分针的夹角为.

查看试题解析
15. 若代数式2x²+3x+7的值是8，则代数式4x²+6x+15的值是。

查看试题解析
16. 如图，点A、点B在数轴上表示的数分别是-4和4.若在数轴上存在一点P到A的距离是点P到B的距离的3倍，则点P所表示的数是 .

查看试题解析

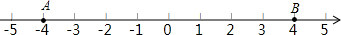
三、综合题

17. 计算：

(1)、 $-$ 1²+ $\sqrt{4} - \sqrt[3]{\frac{8}{27}}$ $\times$ 3

(2)、(-36) $\times$ ( $\frac{1}{4} - \frac{1}{36} + \frac{1}{9}$ )

查看试题解析
18. 解方程

(1)、5(1－x)= －4x+2

(2)、 $\frac{x}{2} - \frac{5 + x}{3} = 1$

查看试题解析
19. 如图，已知平面上有三点A， B， C

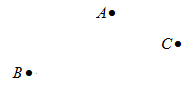
( 1 )按要求画图：画线段AB，直线BC；

( 2 )在线段BC上找一点E，使得CE=BC-AB；

( 3 )过点A做BC的垂线，垂足为点D，找出AB，AC，AD，AE中最短的线段，并说明理由.

查看试题解析
20. 先化简，再求值： $2 a b^{2} - [a^{3} b + 2 (a b^{2} - \frac{1}{2} a^{3} b)] - 5 a^{3} b$ ，其中 $a = - 2$ ， $b = \frac{1}{5}$ ．

查看试题解析
21. 如图所示，两种长方形断桥铝窗框，已知窗框的长都是 $y$ 米，宽都是 $x$ 米，已知一用户需A型的窗框4个，B型的窗框3个．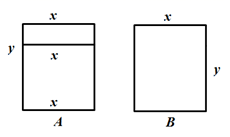

(1)、用含 $x$ 、 $y$ 的式子表示共需断桥铝的长度（窗框本身宽度忽略不计）

(2)、若1米断桥铝的平均费用为200元，求当 $x = 1.5$ ， $y = 2.5$ 时，（1）中断桥铝的总费用为多少元？

查看试题解析
22. 如图，直线 $A B$ 与 $C D$ 相交于点O， $O E$ 平分 $∠ B O D$ ， $O F ⊥ C D$ ．

(1)、若 $∠ E O F = 54 °$ ，求 $∠ A O C$ 的度数；

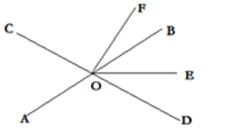(2)、在 $∠ A O D$ 的内部作射线 $O G ⊥ O E$ ，探究 $∠ A O G$ 与 $∠ E O F$ 之间有怎样的关系？并说明理由．

查看试题解析
23. 某学校班主任暑假带领该班三好学生去旅游，甲旅行社说：“如果教师买全票一张，其余学生享受半价优惠；”乙旅行社说：“教师在内全部按票价的6折优惠；”若全部票价是240元.

(1)、如果有10名学生，应参加哪个旅行社，并说出理由；

(2)、当学生人数是多少时，两家旅行社收费一样多？

查看试题解析
24. 已知在数轴上，一动点P从原点出发向左移动4个单位长度到达点A，再向右移动7个单位长度到达点B．

(1)、求点A、B表示的数；

(2)、数轴上是否存在点P，使点P到点A和点B的距离之和为9，若存在，写出点P 表示的数；若不存在，说明理由；

(3)、若小虫M从点A出发，以每秒0.5个单位长度沿数轴向右运动，另一只小虫N从点B出发，以每秒0.2个单位长度沿数轴向左运动．设两只小虫在数轴上的点C处相遇，点C表示的数是多少？

查看试题解析