浙江省宁波市2020-2021学年七年级上学期数学期末模拟试卷
试卷更新日期:2021-01-06 类型:期末考试
一、单选题
-
1. -2020 的相反数是( )A、-2020 B、2020 C、 D、2. 下列计算中,正确的是( )A、 B、 C、 D、3. 地球半径为6370千米,用科学记数法表示为( )A、6.37×10千米 B、6.37×103千米 C、63.7×102千米 D、6.37×104千米4. 下列各数是无理数的是( )A、0.101 B、 C、 D、 -15. 已知ax=ay,下列等式变形不一定成立的是( )A、b+ax=b+ay B、x=y C、x﹣ax=x﹣ay D、 =6. 若∠α的补角为60°,∠β的余角为60°,则∠α和∠β的大小关系是( )A、 B、 C、 D、无法确定7. 如图,数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD.若A,D两点所表示的数分别是﹣5和6,则线段BD的中点所表示的数是( )
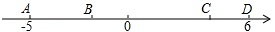 A、6 B、5 C、3 D、28. 我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑 里,驽马每天跑 里. 良马和驽马从同地出发,驽马先走 天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为
A、6 B、5 C、3 D、28. 我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑 里,驽马每天跑 里. 良马和驽马从同地出发,驽马先走 天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为 天,则可列方程为( ) A、 B、 C、 D、9. 对于任意非零实数a, b,定义运算“※"如下: "a※b" = ,则1※2+ 2※3+ 3※4+…+ 2019※2020的值为( )A、 B、 C、 D、10. 如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l . 若知道l的值,则不需要测量就能知道周长的正方形的标号为( )
天,则可列方程为( ) A、 B、 C、 D、9. 对于任意非零实数a, b,定义运算“※"如下: "a※b" = ,则1※2+ 2※3+ 3※4+…+ 2019※2020的值为( )A、 B、 C、 D、10. 如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l . 若知道l的值,则不需要测量就能知道周长的正方形的标号为( ) A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
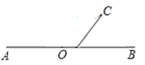
11. 81的算术平方根为.12. 如图,过直线 上一点 画射线 ,则 的度数为 .
 13. 若 与 是同类项,则 = .14. 已知|3x-6|+(2y-4)2=0,则2x-y的值是。15. 皓然同学从油条的制作中受到启发,设计了一个数学问题,如图,在数轴上截取从原点到1的对应点的线段 ,对折后(点 与点 重合),固定左端向右均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如,在一次操作后,原线段 上 , 均变成 ; 变成1;等等),那么在线段 上(除点 , 外)的点中,在第二次操作后,恰好被拉到与1重合的点所对应的数字之和为 .
13. 若 与 是同类项,则 = .14. 已知|3x-6|+(2y-4)2=0,则2x-y的值是。15. 皓然同学从油条的制作中受到启发,设计了一个数学问题,如图,在数轴上截取从原点到1的对应点的线段 ,对折后(点 与点 重合),固定左端向右均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如,在一次操作后,原线段 上 , 均变成 ; 变成1;等等),那么在线段 上(除点 , 外)的点中,在第二次操作后,恰好被拉到与1重合的点所对应的数字之和为 .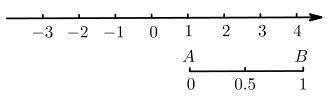 16. 若a,b,c都不为0,则 的值可能是 .
16. 若a,b,c都不为0,则 的值可能是 .三、综合题
-
17. 计算:(1)、(2)、18. 解方程(1)、(2)、19. 先化简,再求值: ,其中 .20. 根据下列语句,画出图形.
如图,已知平面内有四个点 、 、 、 ,共中任意三点都不在同一直线上.
①画直线 ;
②连接 、 ,相交于点 ;
③画射线 、 ,交于点 ;
④过点 作 所在直线的垂线段,垂足为点
 21. 小亮用 元钱买了 支钢笔,准备以一定的价格出售,如果每支钢笔以 元的价格为标准,超过的记作正数,不足的记作负数,记录如下:
21. 小亮用 元钱买了 支钢笔,准备以一定的价格出售,如果每支钢笔以 元的价格为标准,超过的记作正数,不足的记作负数,记录如下:, , , , , , , , , .
(1)、这 支钢笔的最高售价和最低售价各是几元?(2)、当小亮卖完钢笔后是盈利还是亏损?22. 如图,已知数轴上两点A , B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离. (1)、求AB的值;(2)、若在数轴上存在一点C , 使AC=3BC , 求点C表示的数;(3)、在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B , 两个点同时停止运动.设点A运动的时间为t , 在此过程中存在t使得AC=3BC仍成立,求t的值.23. 某电器上销售一种微波炉和电磁炉,微波炉每台定价 元,电磁炉每台定价 元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;
(1)、求AB的值;(2)、若在数轴上存在一点C , 使AC=3BC , 求点C表示的数;(3)、在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B , 两个点同时停止运动.设点A运动的时间为t , 在此过程中存在t使得AC=3BC仍成立,求t的值.23. 某电器上销售一种微波炉和电磁炉,微波炉每台定价 元,电磁炉每台定价 元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的 付款;
现某客户要到该卖场购买微波炉 台,电磁炉 台
(1)、若该客户按方案一、方案二购买,分别需付款多少元?(用含 的式子表示)(2)、若 ,通过计算说明此时那种方案购买较为核算?(3)、当 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?24. 已知OC是∠AOB内部的一条射线,M , N分别为OA , OC上的点,线段OM , ON同时分别以30°/s , 10°/s的速度绕点O逆时针旋转,设旋转时间为t秒.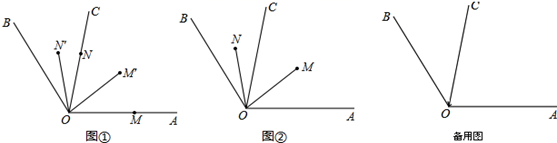 (1)、如图①,若∠AOB=120°,当OM、ON逆时针旋转到OM′、ON′处,若OM , ON旋转时间t为2时,则∠BON′+∠COM′=°;(2)、若OM′平分∠AOC , ON′平分∠BOC , 求∠M′ON′的值;(3)、如图②,若∠AOB=4∠BOC , OM , ON分别在∠AOC , ∠BOC内部旋转时,请猜想∠COM与∠BON的数量关系,并说明理由.(4)、若∠AOC=80°,OM , ON在旋转的过程中,当∠MON=20°,t= .
(1)、如图①,若∠AOB=120°,当OM、ON逆时针旋转到OM′、ON′处,若OM , ON旋转时间t为2时,则∠BON′+∠COM′=°;(2)、若OM′平分∠AOC , ON′平分∠BOC , 求∠M′ON′的值;(3)、如图②,若∠AOB=4∠BOC , OM , ON分别在∠AOC , ∠BOC内部旋转时,请猜想∠COM与∠BON的数量关系,并说明理由.(4)、若∠AOC=80°,OM , ON在旋转的过程中,当∠MON=20°,t= .