浙江省台州市2020-2021学年七年级上学期数学期末模拟试卷
试卷更新日期:2021-01-06 类型:期末考试
一、单选题
-
1. 下列各数种,比 小的数是( )A、 B、 C、0 D、32. 下列各式是一元一次方程的是( )A、x2-2x=1 B、x-1= C、y+3=x-4 D、 =13. 下列不是同类项的是( )A、 和 B、 和 C、 和 D、 和4. 下列说法:①经过一点有无数条直线;②两点之间线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则点M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为( )A、1个 B、2个 C、3个 D、4个5. 如图是一个正方体展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得他们折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为( )
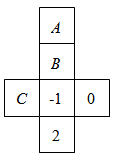 A、1,-2,0 B、0,-2,1 C、-2,0,1 D、-2,1,06.
A、1,-2,0 B、0,-2,1 C、-2,0,1 D、-2,1,06.轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )
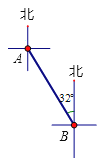
 A、南偏西32° B、南偏东32° C、南偏西58° D、南偏东58°7. 下列变形中,正确的是( )A、若ac=bc,那么a=b B、若 ,那么a=b C、若|a|=|b|,那么a=b D、若 ,那么a=b8. 某班有52人,其中男生的人数比女生人数的2倍少11人,设女生有 人,根据题意可列方程( )A、 B、 C、 D、9. 已知有理数a,b,c在数轴上的位置如图所示,下列结论正确的是( )
A、南偏西32° B、南偏东32° C、南偏西58° D、南偏东58°7. 下列变形中,正确的是( )A、若ac=bc,那么a=b B、若 ,那么a=b C、若|a|=|b|,那么a=b D、若 ,那么a=b8. 某班有52人,其中男生的人数比女生人数的2倍少11人,设女生有 人,根据题意可列方程( )A、 B、 C、 D、9. 已知有理数a,b,c在数轴上的位置如图所示,下列结论正确的是( ) A、 B、 C、 D、10. 已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数…依此类推,那么 的值是( )A、-3 B、 C、 D、
A、 B、 C、 D、10. 已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数…依此类推,那么 的值是( )A、-3 B、 C、 D、二、填空题
-
11. 如果a、b互为相反数,x、y互为倒数,那么(a+b) ﹣2015xy= .12. 已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为 .13. 已知多项式 ,它是次三项式,最高次项的系数 , 常数项为 .14. 如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于度
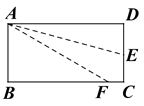 15. 已知代数式a2+a的值是1,则代数式2a2+2a+2018值是 .16. 按如图所示的程序计算,若开始输入的 的值为 我们发现第一次得到的结果为 第 次得到的结果为 …,请你探索第 次得到的结果为 .
15. 已知代数式a2+a的值是1,则代数式2a2+2a+2018值是 .16. 按如图所示的程序计算,若开始输入的 的值为 我们发现第一次得到的结果为 第 次得到的结果为 …,请你探索第 次得到的结果为 .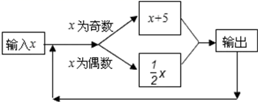
三、综合题
-
17. 计算:(1)、 ;(2)、 .18. 解方程(1)、(2)、19. 已知|x+2|+(y-3)2=0,先化简,再求值:20. 某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元;经粗加工后销售,每吨利润4000元;经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果对蔬菜进行精加工,每天可加工6吨;但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜
全部销售或加工完毕.为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,请说说理由.
21. 你能很快计算出 吗?为了解决这个问题,我们来考察个位为5的自然数的平方,任意一个个位为5的自然数都可以写成10n+5的形式,于是原题即求 的值.N为自然数,分析n=1,n=2,n=3,……这些简单情况,从中探索其规律,并归纳、猜想出结论.
(1)、通过计算、探索规律: = = =(2)、从(1)小题的结果,归纳、猜想得: =(3)、根据上面的归纳、猜想,请计算出 =22. 对于有理数a,b,定义一种新运算“★”,规定a★b . (1)、计算:3★ 的值;(2)、当a,b在数轴上的位置如图所示时,化简:a★b.23. 如图所示, 和 都是直角.
(1)、计算:3★ 的值;(2)、当a,b在数轴上的位置如图所示时,化简:a★b.23. 如图所示, 和 都是直角.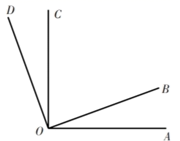 (1)、填空:图中与 互余的角有和;(2)、 与 互补吗?为什么?(3)、若 ,求 与 的度数.24. 综合题
(1)、填空:图中与 互余的角有和;(2)、 与 互补吗?为什么?(3)、若 ,求 与 的度数.24. 综合题如图1, 为直线 上一点,过点O作射线 , ,将一直角三角板( )的直角顶点放在点O处,一边 在射线 上,另一边 与 都在直线 的上方.
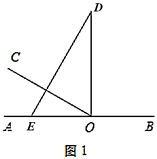 (1)、将图1中的三角板绕点O以每秒 的速度沿顺时针方向旋转一周,如图2,经过t秒后, 恰好平分 .
(1)、将图1中的三角板绕点O以每秒 的速度沿顺时针方向旋转一周,如图2,经过t秒后, 恰好平分 .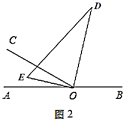
此时t的值为;(直接填空)
(2)、此时 是否平分 ?请说明理由.(3)、在(1)问的基础上,若三角板在转动的同时,射线 也绕O点以每秒 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间 平分 ?请说明理由;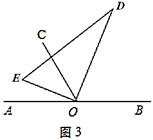 (4)、在(2)问的基础上,经过多长时间 平分 ?
(4)、在(2)问的基础上,经过多长时间 平分 ?