浙江省温州市2020-2021学年八年级上学期数学期末模拟试卷
试卷更新日期:2021-01-06 类型:期末考试
一、单选题
-
1. 在以下的标志中,是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系内,点P(-2,-1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若三角形的三边长分别为2,x,6,则x的值可以是( )A、2 B、4 C、6 D、84. 在平面直角坐标系xOy中,点P(2,1)关于y轴对称的点的坐标是( )A、(﹣2,1) B、(2,1) C、(﹣2,﹣1) D、(2,﹣1)5. 函数 的自变量x的取值范围是( )A、x≥2 B、x≥3 C、x≠3 D、x≥2且x≠36. 对于命题“若 ,则 ”,则下列m值能说明该命题是假命题的是( )A、 B、 C、 D、7. 某个一次函数的图象与直线 平行,并且经过点 ,则这个一次函数的解析式为( )A、 B、 C、 D、8. 如图,∠A=50°,P 是△ABC 内一点,BP 平分 ,CP 平分∠ACB,则∠BPC 的度数为( )
2. 在平面直角坐标系内,点P(-2,-1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若三角形的三边长分别为2,x,6,则x的值可以是( )A、2 B、4 C、6 D、84. 在平面直角坐标系xOy中,点P(2,1)关于y轴对称的点的坐标是( )A、(﹣2,1) B、(2,1) C、(﹣2,﹣1) D、(2,﹣1)5. 函数 的自变量x的取值范围是( )A、x≥2 B、x≥3 C、x≠3 D、x≥2且x≠36. 对于命题“若 ,则 ”,则下列m值能说明该命题是假命题的是( )A、 B、 C、 D、7. 某个一次函数的图象与直线 平行,并且经过点 ,则这个一次函数的解析式为( )A、 B、 C、 D、8. 如图,∠A=50°,P 是△ABC 内一点,BP 平分 ,CP 平分∠ACB,则∠BPC 的度数为( )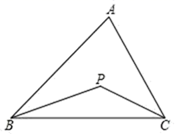 A、100° B、115° C、130° D、140°9. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 与甲车行驶的时间 之间的函数关系如图所示.下列说法错误的是( )
A、100° B、115° C、130° D、140°9. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 与甲车行驶的时间 之间的函数关系如图所示.下列说法错误的是( )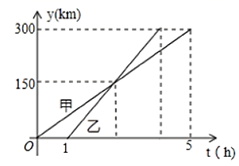 A、 , 两城相距 千米 B、乙车比甲车晚出发 小时,却早到 小时 C、乙车出发后 小时追上甲车 D、在一车追上另一车之前,当两车相距 千米时,10. 如图,△ABC中,AC=BC=1,∠ACB=90°,以AC、BC、AB为边作如图所示的等边△ABD,等边△ACE,等边△BCF,连结DE,DF,则四边形DFCE的面积为( )
A、 , 两城相距 千米 B、乙车比甲车晚出发 小时,却早到 小时 C、乙车出发后 小时追上甲车 D、在一车追上另一车之前,当两车相距 千米时,10. 如图,△ABC中,AC=BC=1,∠ACB=90°,以AC、BC、AB为边作如图所示的等边△ABD,等边△ACE,等边△BCF,连结DE,DF,则四边形DFCE的面积为( )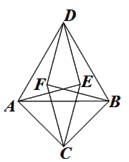 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题
-
11. 已知a>b,则15a+c15b+c(填“>”“<”或“=”).12. 已知△ABC中,∠A∶∠B∶∠C=1∶3∶5,则△ABC的最小内角为°.13. 写一个经过点(-1,0),且y随x增大而增大的一次函数.14. 点E(a,b)到x轴的距离是4,到y轴距离是3,且点E在第四象限,则E点坐标为。15. 如图,在△ABC中,AB=AC=3,AB的垂直平分线分别交AC、AB于点D、E . 若△ABD的周长等于7,则 的长为 .
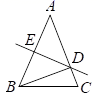 16. 如图,△ABC中,点O是∠ABC、∠ACB角平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=3,求△ABC的面积为 .
16. 如图,△ABC中,点O是∠ABC、∠ACB角平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=3,求△ABC的面积为 .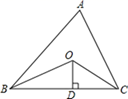 17. 如图,点 的坐标为(-2,0),点 在直线 上运动,当线段 最短时,点 的坐标是.
17. 如图,点 的坐标为(-2,0),点 在直线 上运动,当线段 最短时,点 的坐标是.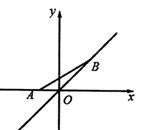 18. 如图在直线上一次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+2S2+2S3+S4= .
18. 如图在直线上一次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+2S2+2S3+S4= .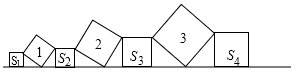
三、综合题
-
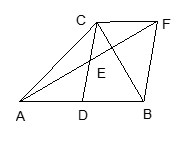
19. 如图.在△ABC中,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连接BF.求证:DB=CF;
 20. 求不等式组 的解集,并把解集在数轴上表示出来.21. 如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上.
20. 求不等式组 的解集,并把解集在数轴上表示出来.21. 如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上. (1)、在图中画出以 为底边的等腰直角三角形 ,点 在小正方形顶点上;(2)、在图中画出以 为腰的等腰三角形 ,点 在小正方形的顶点上,且 的面积为8.连接 ,请直接写出 的长.22. 某水果批发站购进苹果和梨共100箱,其中苹果每箱40元,梨每箱45元。(1)、若设苹果箱数为x箱,总费用为y元,试用x的代数式来表示总费用y.(2)、若购进的100箱水果中,苹果箱数不小于30箱,且不大于90箱,试求该水果批发站此次购入水果的总费用的范围.23. 如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,E、F分别是BD、AC的中点.
(1)、在图中画出以 为底边的等腰直角三角形 ,点 在小正方形顶点上;(2)、在图中画出以 为腰的等腰三角形 ,点 在小正方形的顶点上,且 的面积为8.连接 ,请直接写出 的长.22. 某水果批发站购进苹果和梨共100箱,其中苹果每箱40元,梨每箱45元。(1)、若设苹果箱数为x箱,总费用为y元,试用x的代数式来表示总费用y.(2)、若购进的100箱水果中,苹果箱数不小于30箱,且不大于90箱,试求该水果批发站此次购入水果的总费用的范围.23. 如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,E、F分别是BD、AC的中点. (1)、请你猜想EF与AC的位置关系,并给予证明;(2)、当AC=16,BD=20时,求EF的长.24. 如图,在平面直角坐标系中,A 为 轴上的一动点,B(0,3), BAC= ,AB=AC.
(1)、请你猜想EF与AC的位置关系,并给予证明;(2)、当AC=16,BD=20时,求EF的长.24. 如图,在平面直角坐标系中,A 为 轴上的一动点,B(0,3), BAC= ,AB=AC.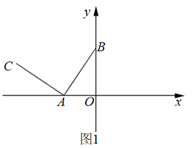
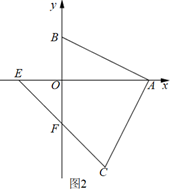
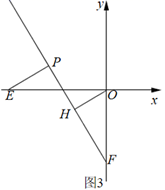 (1)、如图1,若 ,点C在第二象限,求C点坐标;(2)、如图2,当点C在第四象限时,点F与点B关于 轴对称,连接CF并延长交 轴于点E,求点E坐标;(3)、如图3,P 为第二象限的点,点H 在线段PF上,且 ,当点E在 轴负半轴上,点F在y轴负半轴上运动时,且OE=OF,求m、n之间的数量关系.
(1)、如图1,若 ,点C在第二象限,求C点坐标;(2)、如图2,当点C在第四象限时,点F与点B关于 轴对称,连接CF并延长交 轴于点E,求点E坐标;(3)、如图3,P 为第二象限的点,点H 在线段PF上,且 ,当点E在 轴负半轴上,点F在y轴负半轴上运动时,且OE=OF,求m、n之间的数量关系.