浙江省台州市2020-2021学年八年级上学期数学期末模拟试卷

试卷更新日期：2021-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $\frac{2 x}{\sqrt{1 - x}}$ 在实数范围内意义，那么x的取值范围是（）

A、x≥1 B、x>1 C、x≤1 D、x<1

查看试题解析
3. 2020年疫情的影响，人类的健康备注关注。同时我们生存的环境雾霾天气引发关注，宽空气中漂浮着大量的粉尘颗粒，若某各粉尘颗粒的直径约为0.0000065米，则0.0000065用科学记数法表示为（）

A、6.5×10^－⁵ B、6.5×10^－⁶ C、6.5×10^－⁷ D、65×10^－⁶

查看试题解析
4. 下列运算错误的是（）

A、b²·b³=b⁵ B、(a-b)(b+a)=a²-b² C、a⁵+a⁵=a¹⁰ D、(-a²b)²=b²a⁴

查看试题解析
5. 如图，AB=AD ， CB=CD ， AC ， BD相交于点O ，则下列结论正确的是（）

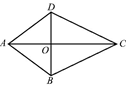A、OA=OC B、点O到AB ， CD的距离相等 C、∠BDA=∠BDC D、点O到CB ， CD的距离相等

查看试题解析
6. 已知正多边形的一个外角等于 $40 °$ ，则这个正多边形的内角和的度数为（）

A、 $1440 °$ B、 $1260 °$ C、 $1080 °$ D、 $900 °$

查看试题解析
7. 小慧与小秀去距学校10千米的博物馆参观，小慧骑自行车先走，过了30分钟后，小秀乘汽车出发，结果她们同时到达，已知汽车的速度是骑车速度的4倍.设骑车的速度为x千米/小时，则所列方程正确的是（）

A、 $\frac{10}{x} - \frac{10}{4 x} = 30$ B、 $\frac{10}{4 x} - \frac{10}{x} = 30$ C、 $\frac{10}{x} - \frac{10}{4 x} = \frac{1}{2}$ D、 $\frac{10}{4 x} - \frac{10}{x} = \frac{1}{2}$

查看试题解析
8. 如图所示，小兰用尺规作图作△ABC边AC上的高BH ，作法如下：
①分别以点DE为圆心，大于DE的一半长为半径作弧两弧交于F；②作射线BF ，交边AC于点H；③以B为圆心，BK长为半径作弧，交直线AC于点D和E；④取一点K使K和B在AC的两侧；所以BH就是所求作的高．其中顺序正确的作图步骤是（）

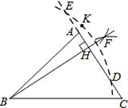A、①②③④ B、④③①② C、②④③① D、④③②①

查看试题解析
9. 已知 $\frac{1}{x} - \frac{1}{y} = 5$ ，则代数式 $\frac{3 x - 20 x y - 3 y}{x - 2 x y - y}$ 的值为（）

A、 $5$ B、 $- \frac{5}{3}$ C、 $\frac{5}{7}$ D、 $- \frac{35}{3}$

查看试题解析
10. 已知AC平分∠DAB ， CE⊥AB于E ， AB=AD+2BE ，则下列结论：①2AE=AB+AD；②CD=CB；③∠DAB+∠DCB=180°；④S_△ACE=S_△BCE+S_△ADC ．其中正确结论的个数是（）

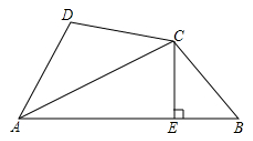A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

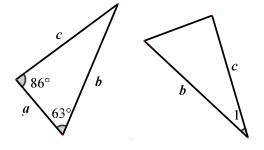
11. 因式分解：4ax²﹣4ay²= ．

查看试题解析
12. 如图，两个三角形全等，图中的字母表示三角形的边长，则∠1= 。

查看试题解析
13. 如图，D，E分别是边BC， AD上的中点，若S_阴影面积=2，则△ABC的面积是。

查看试题解析
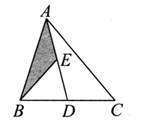14. 当m＝时，分式方程 $\frac{x - 2}{x - 3} = \frac{m}{3 - x}$ 会出现增根

查看试题解析
15. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（a，b），经过第1次变换后所得的 $A_{1}$ 坐标是 $(a ， - b)$ ，则经过第2020次变换后所得的点 $A_{2020}$ 坐标是.

查看试题解析
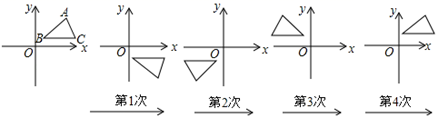16. E、F是线段AB上的两点，且AB＝16，AE＝1，BF＝3，点G是线段EF上的一动点，分别以AG、BG为斜边在AB同侧作两个等腰直角三角形，直角顶点分别为D、C，如图所示，连接CD并取中点P，连结PG，点G从E点出发运动到F点，则线段PG扫过的图形面积为.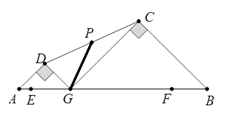

查看试题解析

三、综合题

17.

(1)、分解因式 $x^{2} + 2 x - 3$ ；

(2)、利用因式分解计算： $3.68 \times 15.7 - 31.4 + 15.7 \times 0.32$ ．

查看试题解析
18. 沿着图中的虚线，用四种不同的方法将下面的图形分成两个全等的图形

查看试题解析
19. 如图，四边形ABCD中，点E在边CD上，连结AE、BE．已知：AD//BC；DE=CE；∠1=∠2；

求证：

(1)、∠3=∠4；

(2)、求证：AD+BC=AB．

查看试题解析
20. 老师在黑板上书写了一个代数式的正确计算结果，随后用字母A代替了原代数式的一部分，如下： $(A - \frac{x^{2} - 1}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1} = \frac{x + 1}{x - 1}$

(1)、求代数式A，并将其化简；

(2)、原代数式的值能等于 $- 1$ 吗？请说明理由.

查看试题解析
21. 全国在抗击新冠肺炎疫情期间，甲乙两家公司共同参与一项建造有1800个床位的方舱医院的工程，已知甲乙两家公司，每小时建造床位的数量之比为3：2，并且甲公司单独完成此项工程，比乙公司单独完成此项工程要少用20小时．

(1)、分别求甲乙两家公司每小时改建床位的数量？

(2)、甲乙两家公司合作完成该项工程，若要求乙公司的工作时间不得少于甲公司工作时间的1/2，求乙公司至少工作多少小时？

查看试题解析
22. 请认真观察图形，解答下列问题：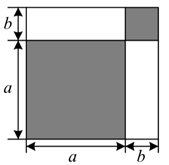

(1)、根据图中条件，试用两种不同方法表示阴影部分的面积.
方法1：；方法2：.

(2)、从中你能发现什么结论？请用乘法公式表示该结论：.

(3)、运用你所得到的结论，解决问题：已知 ${(x + y)}^{2} = 25 ， \frac{1}{2} x y = 3 ，$ 求 $x^{2} + y^{2}$ 的值.

查看试题解析
23. 如图1，在△ABC中，AE⊥BC于，AE=BE，D是AE上的一点，且DE=CE，连接BD、AC．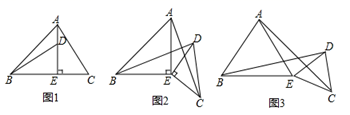

(1)、试判断BD与AC的位置关系和数量关系，并说明理由；

(2)、如图2，若将△DCE绕点E旋转一定的角度后，仍然有DE⊥EC，DE=CE，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；

(3)、如图3，若将(2)中的等腰直角三角形都换成等边三角形，其他条件不变：
①试猜想BD与AC的数量关系，并说明理由；

②你能求出BD与AC所成的角的度数吗？如果能，请直接写出该角的度数；如果不能，请说明理由．

查看试题解析
24. 已知在四边形ABCD中，∠ABC+∠ADC=180°，AB=BC．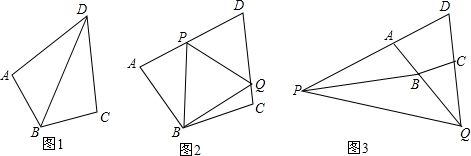

(1)、如图1，若∠BAD=90°，AD=2，求CD的长度；

(2)、如图2，点P、Q分别在线段AD、DC上，满足PQ=AP+CQ，求证：∠PBQ=90°− $\frac{1}{2}$ ∠ADC；

(3)、如图3，若点Q运动到DC的延长线上，点P也运动到DA的延长线上时，仍然满足PQ=AP+CQ，则（2）中的结论是否成立？若成立，请给出证明过程，若不成立，请写出∠PBQ与∠ADC的数量关系，并给出证明过程.

查看试题解析