浙江省丽水市2020-2021学年八年级上学期数学期末模拟试卷
试卷更新日期:2021-01-05 类型:期末考试
一、单选题
-
1. 在平面直角坐标系内,下列各点中在第二象限的点是( )A、( 3,2) B、( 3,-2) C、( -3,2) D、( -2,-3)2. 下列四个图形中,线段BE是 的高的图形是( )A、
 B、
B、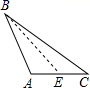 C、
C、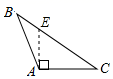 D、
D、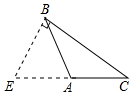 3. 在数轴上表示不等式 ,正确的是( )A、
3. 在数轴上表示不等式 ,正确的是( )A、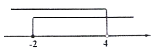 B、
B、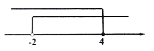 C、
C、 D、
D、 4. 在等腰△ABC 中,AB=AC,中线 BD将这个三角形的周长分为 15和12 两个部分,则这个等腰三角形的底边长为( )A、7 B、10 C、7 或 11 D、7 或 105. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
4. 在等腰△ABC 中,AB=AC,中线 BD将这个三角形的周长分为 15和12 两个部分,则这个等腰三角形的底边长为( )A、7 B、10 C、7 或 11 D、7 或 105. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( ) A、AB=DE B、AC=DF C、BF=EC D、∠B=∠E6. 在Rt△ABC中,∠C=90°,AB=10,BC=8,则AC=( )A、4 B、5 C、6 D、77. 已知a<b,则下列四个不等式中,不正确的是( )A、a+2<b+2 B、 C、 D、8. 已知一次函数y=(m+1)x+n-2的图象经过一.三.四象限,则m,n的取值范围是( )A、m>-1,n>2 B、m<-1,n>2 C、m>-1,n<2 D、m<-1,n<29. 如图,是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多反射),则该球最后将落入的球袋是( )
A、AB=DE B、AC=DF C、BF=EC D、∠B=∠E6. 在Rt△ABC中,∠C=90°,AB=10,BC=8,则AC=( )A、4 B、5 C、6 D、77. 已知a<b,则下列四个不等式中,不正确的是( )A、a+2<b+2 B、 C、 D、8. 已知一次函数y=(m+1)x+n-2的图象经过一.三.四象限,则m,n的取值范围是( )A、m>-1,n>2 B、m<-1,n>2 C、m>-1,n<2 D、m<-1,n<29. 如图,是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多反射),则该球最后将落入的球袋是( )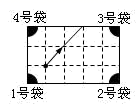 A、1 号袋 B、2 号袋 C、3 号袋 D、4 号袋10. 将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )
A、1 号袋 B、2 号袋 C、3 号袋 D、4 号袋10. 将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )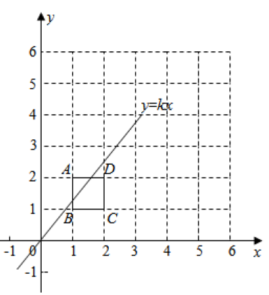 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
11. 点M(3,4)关于x轴的对称点N的坐标是;12. 根据数量“ 的 倍与 的和大于 ”,列不等式为 .13. 一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是 .
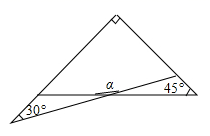 14. 如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC , 垂足为D , △ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 .
14. 如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC , 垂足为D , △ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 .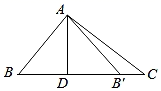 15. 如图,在 中, 面积为 , 的垂直平分线 分别交 , 于点 .若点D为 的中点,点P为线段 上一动点,则 周长的最小值为 .
15. 如图,在 中, 面积为 , 的垂直平分线 分别交 , 于点 .若点D为 的中点,点P为线段 上一动点,则 周长的最小值为 .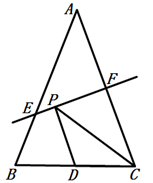 16. 如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2019次,点P依次落在点P1、P2、P3、…、P2019的位置,则点P2019的横坐标为.
16. 如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2019次,点P依次落在点P1、P2、P3、…、P2019的位置,则点P2019的横坐标为.
三、综合题
-
17. 解下列不等式和不等式组.(1)、2(x+1)>3x-4;(2)、18. 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
 (1)、画出△ABC关于x轴的对称图形△A1B1C1;写出A1 , B1 , C1的坐标.(2)、将△A1B1C1沿x轴方向向左平移3个单位长度后得到△A2B2C2 , 写出顶点A2 , B2 , C2的坐标.19. 已知y+1与x成正比例,并且当x=2时y=-3.(1)、求y与x的函数表达式;(2)、当x=-1时,求y的值.20. 如图,在 中, ,DH垂直平分BC交AB于点D,BE平分 ,且 于点E,与CD相交于点F.
(1)、画出△ABC关于x轴的对称图形△A1B1C1;写出A1 , B1 , C1的坐标.(2)、将△A1B1C1沿x轴方向向左平移3个单位长度后得到△A2B2C2 , 写出顶点A2 , B2 , C2的坐标.19. 已知y+1与x成正比例,并且当x=2时y=-3.(1)、求y与x的函数表达式;(2)、当x=-1时,求y的值.20. 如图,在 中, ,DH垂直平分BC交AB于点D,BE平分 ,且 于点E,与CD相交于点F. (1)、求证:BF=AC;(2)、求证: .21. 如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD//BE,∠GBE的平分线与AD交于点D,连接CD.
(1)、求证:BF=AC;(2)、求证: .21. 如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD//BE,∠GBE的平分线与AD交于点D,连接CD.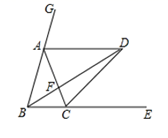 (1)、求证:①AB=AD;②CD平分∠ACE.(2)、猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.22. 随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的 A、B两种型号的净水器 ,下表是近两周的销售情况:
(1)、求证:①AB=AD;②CD平分∠ACE.(2)、猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.22. 随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的 A、B两种型号的净水器 ,下表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号:
B种型号:
第一周
3台
5台
18000元
第二周
4台
10台
31000元
(1)、求A, B两种型号的净水器的销售单价.(2)、若电器公司准备用不多于54000元的金额采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?23. 如图,在 中, ,AE平分∠BAC,BD⊥AC于D,E为BC 边上一点,AE、BD交于点F,EG//BD.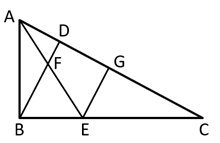 (1)、求证:AB=AG;(2)、当 时,在 上有一动点 ,求 的最小值.24. 利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.
(1)、求证:AB=AG;(2)、当 时,在 上有一动点 ,求 的最小值.24. 利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.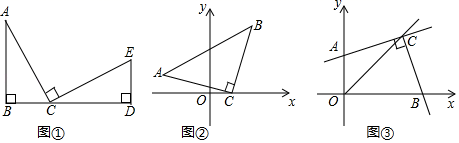 (1)、如图①,B , C , D三点共线,AB⊥BD于点B , DE⊥BD于点D , AC⊥CE , 且AC=CE . 若AB+DE=6,求BD的长.(2)、如图②,在平面直角坐标系中,△ABC为等腰直角三角形,直角顶点C的坐标为(1,0),点A的坐标为(﹣2,1).求直线AB与y轴的交点坐标.(3)、如图③,∠ACB=90°,OC平分∠AOB , 若点B坐标为(b , 0),点A坐标为(0,a).则S四边形AOBC= . (只需写出结果,用含a , b的式子表示)
(1)、如图①,B , C , D三点共线,AB⊥BD于点B , DE⊥BD于点D , AC⊥CE , 且AC=CE . 若AB+DE=6,求BD的长.(2)、如图②,在平面直角坐标系中,△ABC为等腰直角三角形,直角顶点C的坐标为(1,0),点A的坐标为(﹣2,1).求直线AB与y轴的交点坐标.(3)、如图③,∠ACB=90°,OC平分∠AOB , 若点B坐标为(b , 0),点A坐标为(0,a).则S四边形AOBC= . (只需写出结果,用含a , b的式子表示)