浙江省宁波市2020-2021学年八年级上学期数学期末模拟试卷

试卷更新日期：2021-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一个三角形的两边长分别为4和7，则此三角形的第三边的取值可能是（）

A、4 B、3 C、2 .1

查看试题解析
3. 已知a＞b，则下列不等式中正确的是（）

A、﹣2a＞﹣2b B、 $\frac{a}{2} < \frac{b}{2}$ C、2﹣a＞2﹣b D、a+2＞b+2

查看试题解析
4. 如图，用“SAS”证明△ABC≌△ADE，若已知AB＝AD，AC＝AE，则还需添加条件为（）

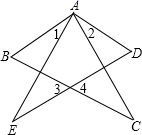A、∠B＝∠D B、∠C＝∠E C、∠1＝∠2 D、∠3＝∠4

查看试题解析
5. 已知点M（3，－1）关于y轴对称的的对称点N的坐标为（a＋b，1－b），则a^b的值为（）

A、10 B、25 C、－3 D、32

查看试题解析
6. 直线y＝2x﹣1沿y轴向下平移3个单位，则平移后直线与x轴的交点坐标为（）

A、（﹣2，0） B、（2，0） C、（4，0） D、（﹣1，0）

查看试题解析
7. 如图，△ABC 中，AB = 6cm ，AC = 8cm ，BC 的垂直平分线l 与 AC 相交于点 D ，则△ABD 的周长为（）

A、10cm B、12cm C、14cm D、16cm

查看试题解析
8. 如图，在等边△ABC中，点E是AC边的中点，点P是△ABC的中线AD上的动点，且AD=6，则EP+CP的最小值是（）

A、12 B、9 C、6 D、3

查看试题解析
9. 若不等式组 ${\begin{matrix} \end{matrix} \begin{matrix} x + 2 > 2 x - 6 \\ x < m \end{matrix}$ 的解为 $x < 8$ ，则m的取值范围是（）

A、 $m \geq 8$ B、 $m \leq 8$ C、 $m < 8$ D、 $m > 8$

查看试题解析
10. 如图，已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（10，0），点B（0，6），点P为BC边上的动点，将△OBP沿OP折叠得到△OPD，连接CD、AD.则下列结论中：①当∠BOP＝45°时，四边形OBPD为正方形；②当∠BOP＝30°时，△OAD的面积为15；③当P在运动过程中，CD的最小值为2 $\sqrt{34}$ ﹣6；④当OD⊥AD时，BP＝2.其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知“ $x$ 的4倍小于3”，将这一数量关系用不等式表示是.

查看试题解析
12. 将命题“有一个内角是直角的三角形是直角三角形”改写成如果……那么……的形式．

查看试题解析
13. 点A（﹣2，﹣4）到x轴的距离为．

查看试题解析
14. 若一次函数 $y = (k - 1) x + k + 2$ 的图像不经过第三象限，则k的取值范围是．

查看试题解析
15. 等腰三角形的周长是24cm，其中一边长是10cm，则腰长为．

查看试题解析
16. 在平面直角坐标系中，已知一次函数 $y = 2 x + 1$ 的图象经过 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ 两点，若 $x_{1} < x_{2}$ ，则 $y_{1}$ $y_{2}$ .（填”>”，”<”或”=”）

查看试题解析
17. 如图，直线 $y = - \frac{3}{4} x + 3$ 与 $x$ 轴、 $y$ 轴分别相交于点A、B，点M在x轴上且不同于点A，点N是平面直角坐标系中的第一象限内任意一点.如果以A，B，M，N为顶点的四边形是菱形，那么满足条件的点M的坐标是.

查看试题解析
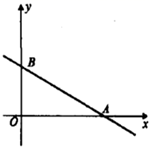18. 如图，在矩形ABCD中，AB＝2，AD＝3，E为BC边上一动点，作EF⊥AE，且EF＝AE．连接DF，AF．当DF⊥EF时，△ADF的面积为．

查看试题解析

三、综合题

19. 解下列不等式（组）:

(1)、 $\frac{x + 5}{2} - 1 < \frac{3 x + 2}{2}$

(2)、 ${\begin{cases} 3 x + 2 \leq 2 (x + 3) \\ \frac{2 x - 1}{3} > \frac{x}{2} \end{cases}$ .

查看试题解析
20. 如图，四边形ABCD中，点E在边CD上，连结AE、BE．已知：AD//BC；DE=CE；∠1=∠2；

求证：

(1)、∠3=∠4；

(2)、求证：AD+BC=AB．

查看试题解析
21. 如图，△ABC中，按要求画图：

(1)、画出△ABC中BC边上的中线AD；

(2)、画出△ABC中∠B的平分线BE．

(3)、画出△ABC中AB边上的高CF．

查看试题解析
22. 星期天8：00～8：30，燃气公司给平安加气站的储气罐注入天然气.之后，一位工作人员以每车20立方米的加气量，依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y（立方米）与时间x（小时）的函数关系如图所示.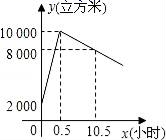

(1)、8：00～8：30，燃气公司向储气罐注入了多少立方米的天然气；

(2)、当x≥0.5时，求储气罐中的储气量y（立方米）与时间x（小时）的函数解析式；

(3)、请你判断，正在排队等候的第18辆车能否在当天10：30之前加完气？请说明理由.

查看试题解析
23. 如图，已知直线y₁=﹣ $\frac{1}{2}$ x+1与x轴交于点A，与直线y₂=﹣ $\frac{3}{2}$ x交于点B．

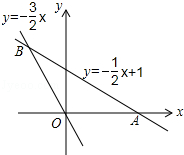(1)、求△AOB的面积；

(2)、求y₁＞y₂时x的取值范围．

查看试题解析
24. 如图所示，已知△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts．

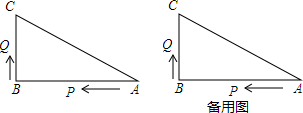(1)、出发3s后，求PB的长；

(2)、当点Q在边BC上运动时，出发多久后，△PQB能形成等腰三角形？

(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析