浙江省金华市2020-2021学年八年级上学期数学期末模拟试卷
试卷更新日期:2021-01-05 类型:期末考试
一、单选题
-
1. 以下列长度的线段为边,能组成三角形的是( )A、3,4,8 B、8,7,15 C、5,6,7 D、3,5,102. 如图,笑脸所在的点的坐标可能是( )
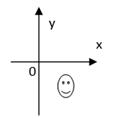 A、(3,2) B、(-3,-2) C、(-3,2) D、(3,-2)3. 如图,边长为4的等边 在平面直角坐标系中的位置如图所示,点 在 轴上,点 , 在 轴上,则点 的坐标为( )
A、(3,2) B、(-3,-2) C、(-3,2) D、(3,-2)3. 如图,边长为4的等边 在平面直角坐标系中的位置如图所示,点 在 轴上,点 , 在 轴上,则点 的坐标为( )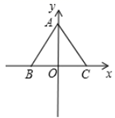 A、 B、 C、 D、4. 如图,小明在A处,小红在B处,小李在C处,AB=10m,BC=8m,则下列说法准确的是( )
A、 B、 C、 D、4. 如图,小明在A处,小红在B处,小李在C处,AB=10m,BC=8m,则下列说法准确的是( )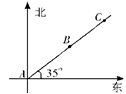 A、小红在小明的北偏东35°方向 B、小红在小明的南偏西55°方向 C、小明在小红的南偏西55°方向,距离为10m处 D、小明在小李的北偏东35°方向,距离为18m处5. 下列四组线段中,不能组成直角三角形的是( )A、 , , B、 , , C、 D、 , ,6. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 > C、x+3>y+3 D、-3x>-3y7. 已知如图,AB=AE,只需再加一个条件就能证明△ABC≌△AED,下列选项是所加条件,请判断哪一个不能判断△ABC≌△AED( )
A、小红在小明的北偏东35°方向 B、小红在小明的南偏西55°方向 C、小明在小红的南偏西55°方向,距离为10m处 D、小明在小李的北偏东35°方向,距离为18m处5. 下列四组线段中,不能组成直角三角形的是( )A、 , , B、 , , C、 D、 , ,6. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 > C、x+3>y+3 D、-3x>-3y7. 已知如图,AB=AE,只需再加一个条件就能证明△ABC≌△AED,下列选项是所加条件,请判断哪一个不能判断△ABC≌△AED( )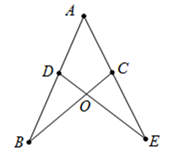 A、∠B=∠E B、AC=AD C、∠ADE=∠ACB D、BC=DE8. 点点与圆圆同学相约去博物馆,点点同学从家步行出发去汽车站,等了圆圆一会儿后再一起乘客车去博物馆,如图是点点同学离开家的路程 (千米)和所用时间 (分)之间的函数关系,则( )
A、∠B=∠E B、AC=AD C、∠ADE=∠ACB D、BC=DE8. 点点与圆圆同学相约去博物馆,点点同学从家步行出发去汽车站,等了圆圆一会儿后再一起乘客车去博物馆,如图是点点同学离开家的路程 (千米)和所用时间 (分)之间的函数关系,则( )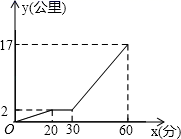 A、点点同学从家到汽车站的步行速度为0.1千米/时 B、点点同学在汽车站等圆圆用了30分钟 C、客车的平均速度是30千米/时 D、圆圆同学乘客车用了20分钟9. 如图,∠C=90°,AD平分∠BAC交BC于D , 若BC=5cm , BD=3cm , 则点D到AB的距离为( )cm .
A、点点同学从家到汽车站的步行速度为0.1千米/时 B、点点同学在汽车站等圆圆用了30分钟 C、客车的平均速度是30千米/时 D、圆圆同学乘客车用了20分钟9. 如图,∠C=90°,AD平分∠BAC交BC于D , 若BC=5cm , BD=3cm , 则点D到AB的距离为( )cm .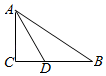 A、3 B、4 C、2 D、110. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
A、3 B、4 C、2 D、110. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )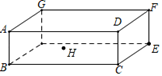 A、 B、17 C、 D、
A、 B、17 C、 D、二、填空题
-
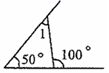
11. 若 的3倍与2的差是负数,则可列出不等式.12. 如图所示,图中的∠1=º.
 13. 请写出“三个角都相等的三角形是等边三角形”的逆命题:.14. 如图的2×5的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有个.
13. 请写出“三个角都相等的三角形是等边三角形”的逆命题:.14. 如图的2×5的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有个. 15. 如图所示,直线y=kx+b经过点(﹣2,0),则关于x的不等式kx+b<0的解集为 .
15. 如图所示,直线y=kx+b经过点(﹣2,0),则关于x的不等式kx+b<0的解集为 .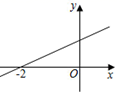 16. 如图所示,AOB是一钢架,设∠AOB=α,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH…,添加的钢管长度都与OE相等,若最多能添加这样的钢管4根,则α的取值范围是.
16. 如图所示,AOB是一钢架,设∠AOB=α,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH…,添加的钢管长度都与OE相等,若最多能添加这样的钢管4根,则α的取值范围是.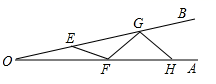
三、综合题
-
17. 解不等式组 (并把解集表示在数轴上,写出所有的整数解).18. 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上.CE=BC,过点E作AC的垂线,交CD的延长线于点F,求证AB=FC.
 19. 如图, , , , ,
19. 如图, , , , , (1)、求证: ;(2)、试求 的度数.20. 一次函数的图象过点(-2,3),(1,3)两点(1)、求出一次函数解析式;(2)、当函数值y满足 时,求自变量x的取值范围;(3)、求该图像与坐标轴围成的三角形的面积.21. 如图,在△ABC中,AB=AC,DE∥AB,分别交BC、AC于点D、E,点F在BC的延长线上,且CF=DE.
(1)、求证: ;(2)、试求 的度数.20. 一次函数的图象过点(-2,3),(1,3)两点(1)、求出一次函数解析式;(2)、当函数值y满足 时,求自变量x的取值范围;(3)、求该图像与坐标轴围成的三角形的面积.21. 如图,在△ABC中,AB=AC,DE∥AB,分别交BC、AC于点D、E,点F在BC的延长线上,且CF=DE.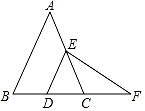 (1)、求证:△CEF是等腰三角形;(2)、连接AD,当AD⊥BC,BC=8,△CEF的周长为16时,求△DEF的周长.22. 如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).
(1)、求证:△CEF是等腰三角形;(2)、连接AD,当AD⊥BC,BC=8,△CEF的周长为16时,求△DEF的周长.22. 如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).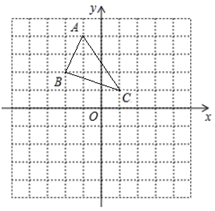 (1)、作ΔABC关于x轴对称的△A1B1C1 , 并写出点A1 , B1 , C1的坐标,(2)、作△ABC关于y轴对称的△A2B2C2 , 并写出点A2 , B2 , C2的坐标,(3)、观察点A1 , B1 , C1和A2 , B2 , C2的坐标,请用文字语言归纳点A1和A2 , B1和B2 , C1和C2坐标之间的关系.23. 某水果批发站购进苹果和梨共100箱,其中苹果每箱40元,梨每箱45元。(1)、若设苹果箱数为x箱,总费用为y元,试用x的代数式来表示总费用y.(2)、若购进的100箱水果中,苹果箱数不小于30箱,且不大于90箱,试求该水果批发站此次购入水果的总费用的范围.24. 在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)、作ΔABC关于x轴对称的△A1B1C1 , 并写出点A1 , B1 , C1的坐标,(2)、作△ABC关于y轴对称的△A2B2C2 , 并写出点A2 , B2 , C2的坐标,(3)、观察点A1 , B1 , C1和A2 , B2 , C2的坐标,请用文字语言归纳点A1和A2 , B1和B2 , C1和C2坐标之间的关系.23. 某水果批发站购进苹果和梨共100箱,其中苹果每箱40元,梨每箱45元。(1)、若设苹果箱数为x箱,总费用为y元,试用x的代数式来表示总费用y.(2)、若购进的100箱水果中,苹果箱数不小于30箱,且不大于90箱,试求该水果批发站此次购入水果的总费用的范围.24. 在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE. (1)、如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=度;(2)、设∠BAC=α,∠DCE=β.
(1)、如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE=度;(2)、设∠BAC=α,∠DCE=β.① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系(不需证明).