浙江省湖州市2020-2021学年八年级上学期数学期末模拟试卷

试卷更新日期：2021-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关系式中，表示y是x的一次函数的是（）

A、 $y = \frac{1}{x}$ B、y=2x C、 $y = \sqrt{x - 1}$ D、 $y = x^{2} + 2 x - 1$

查看试题解析
2. 如图，已知 $B D = C D$ ，则 $A D$ 一定是 $△ A B C$ 的（）

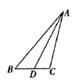A、角平分线 B、高线 C、中线 D、无法确定

查看试题解析
3. 点 $P (3, - 5)$ 关于x轴对称的点的坐标为（）

A、 $(- 3, - 5)$ B、 $(5, 3)$ C、 $(- 3, 5)$ D、 $(3, 5)$

查看试题解析
4. 如图，数轴上点A所表示的数是（）.

A、 $\sqrt{5}$ B、 $- \sqrt{5} - 1$ C、 $\sqrt{5} + 1$ D、 $\sqrt{5} - 1$

查看试题解析
5. 如图，某人把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，最省事的办法是（）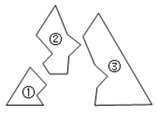

A、带①去 B、带②去 C、带①或②去 D、带③去

查看试题解析
6. 能说明命题“对于任何实数a，都有|a|>-a”是假命题的反例是（）

A、a=-2 B、a= $\frac{1}{2}$ C、a=1 D、a=2

查看试题解析
7. 不等式 $\frac{x}{2} - \frac{x - 1}{3} \geq 1$ 的解集为（）

A、 $x \geq 4$ B、 $x \geq - 1$ C、 $x \geq 8$ D、 $x \geq 3$

查看试题解析
8. 如图，是雷达探测器测得的结果，图中显示在点A，B，C，D，E，F处有目标出现，目标的表示方法为（r，α），其中，r表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．例如，点A，D的位置表示为A（5，30°），D（4，240°）．用这种方法表示点B，C，E，F的位置，其中正确的是（）

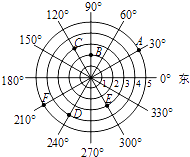A、B（2，90°） B、C（2，120°） C、E（3，120°） D、F（4，210°）

查看试题解析
9. 如图，直线 $y = - x + m$ 与 $y = n x + 4 n (n \neq 0)$ 的交点的横坐标为-2，则关于x的不等式 $- x + m > n x + 4 n > 0$ 的整数解为（）.

A、 $- 1$ B、 $- 5$ C、 $- 4$ D、 $- 3$

查看试题解析
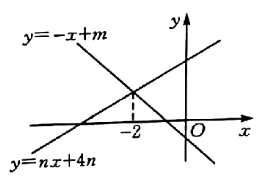10. 如图，两个正方形边长分别为 $a$ 、 $b$ ，如果 $a + b = 18$ ， $a b = 60$ ，则图中阴影部分的面积为（）

A、144 B、72 C、68 D、36

查看试题解析

二、填空题

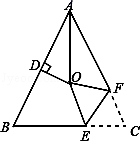
11. 点(2，-3)在第象限

查看试题解析
12. 一次函数y＝2x－6的图象与x轴的交点坐标为.

查看试题解析
13. 某数的一半比它本身的 $\frac{2}{3}$ 大12，若设这个数为x，可列方程为。

查看试题解析
14. 等腰三角形的周长是24cm，其中一边长是10cm，则腰长为．

查看试题解析
15. 不等式6－4x≥3x－8的非负整数解有个.

查看试题解析
16. 如图，在△ABC中，AB=AC，∠BAC=64°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF(E在BC上，F在AC上)折叠，点C与点O恰好重合，则∠OEC为度．

查看试题解析

三、综合题

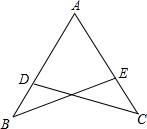
17. 解不等式组 ${\begin{array}{l} \frac{x + 1}{3} > 0 ① \\ 2(x+5) \geq 6(x-1) ② \end{array}$ 并在数轴上表示其解集．

查看试题解析
18. 一次函数 $y = k x + b$ 的图象经过 $(- 2, 1)$ 和 $(1, 4)$ 两点.

(1)、求一次函数的解析式.

(2)、当 $x = 3$ 时，求 $y$ 的值.

查看试题解析
19. 如图，AB＝AC，∠B＝∠C.求证：BE＝CD.

查看试题解析
20. 如图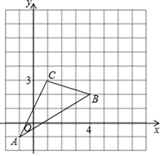

(1)、请写出 $△ A B C$ 各顶点的坐标．

(2)、若把 $△ A B C$ 向上平移2个单位，再向右平移3个单位得到 $△ A_{1} B_{1} C_{1}$ ，请在图中画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标．

(3)、求出 $△ A B C$ 的面积

查看试题解析
21. 如图，在△ABC中，AB=AC ， D在边AC上，且BD=DA=BC ．

(1)、如图1，填空：∠A= ．

(2)、如图2，若M为线段AC上的点，过M作直线MH⊥BD于H ，分别交直线AB、BC于点N、E ．
①求证：△BNE是等腰三角形；

②试写出线段AN、CE、CD之间的数量关系，并说明理由．

查看试题解析
22. 一辆客车从甲地开往乙地，一辆轿车从乙地开往甲地，两车同时出发，两车行驶x小时后，记客车离甲地的距离为y₁千米，轿车离甲地的距离为y₂千米，y₁、y₂关于x的函数图象如图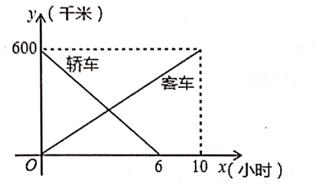

(1)、根据图象，求出y₁、y₂关于x的函数关系式

(2)、当两车相遇时，求此时客车行驶的时间；

(3)、两车相距200千米时，求客车行驶的时间。

查看试题解析
23. 已知点A(8，0)及在第一象限的动点B(x，y)，且x+y＝10，设 $△$ OBA的面积为S．

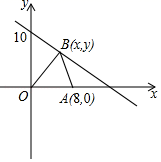(1)、求S关于x的函数关系式，并写出自变量x的取值范围；

(2)、求S＝12时B点坐标；

(3)、在（2）的基础上，设点Q为y轴上一动点，当BQ+AQ的值最小时，求Q点坐标．

查看试题解析
24. 如图，△ABC为等边三角形，边长为6，P ， Q分别为AB ， AC边上的动点，点P ，点Q同时从点A出发，若P以 $\frac{3}{2}$ 个单位每秒的速度从点A向点B运动，点Q以2个单位每秒的速度从点A向点C运动，设运动时间为t ．

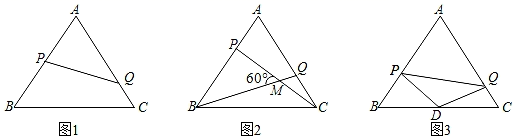(1)、如图1，①当t＝时，P是线段AB的中点，此时线段AQ与AC的数量关系是AQ＝AC ．
②在点P、Q运动过程中，△APQ是否能构成等腰三角形？；

A ．有可能 B ．不可能 C ．无法确定

(2)、如图2，连接CP、BQ交于点M ，请问当t为何值时，∠BMP＝60°；

(3)、如图3，D为BC边上的中点，P ， Q在运动过程中，D ， P ， Q三点是否能构成使∠PDQ＝120°的等腰三角形？若能，试求：
①运动时间t；

②设四边形APDQ的面积为S₁ ， △ABC的面积为S₂ ．请直接写出S₁与S₂的关系式；若不能，请说明理由．

查看试题解析