浙江省杭州市2021届九年级上学期数学期末模拟试卷
试卷更新日期:2021-01-05 类型:期末考试
一、单选题
-
1. 有一个转盘如图,让转盘自由转动两次,则指针两次都落在黄色区域的概率是( )
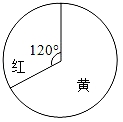 A、 B、 C、 D、2. 如图,在 中, ,若 ,则线段 的长为( )
A、 B、 C、 D、2. 如图,在 中, ,若 ,则线段 的长为( )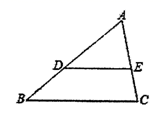 A、3 B、4 C、 D、3. 如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2 , 周长分别是C1与C2 , 则下列说法正确的是( )
A、3 B、4 C、 D、3. 如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2 , 周长分别是C1与C2 , 则下列说法正确的是( )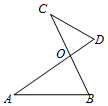 A、 B、 C、 D、4. 在平面直角坐标系中,抛物线y=(x+3)(x﹣1)经过变换后得到抛物线y=(x+1)(x﹣3),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移4个单位 D、向右平移4个单位5. 如图,⊙O是△ABC的外接圆,半径为2cm , 若BC=2cm , 则∠A的度数为( )
A、 B、 C、 D、4. 在平面直角坐标系中,抛物线y=(x+3)(x﹣1)经过变换后得到抛物线y=(x+1)(x﹣3),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移4个单位 D、向右平移4个单位5. 如图,⊙O是△ABC的外接圆,半径为2cm , 若BC=2cm , 则∠A的度数为( )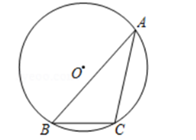 A、30° B、25° C、15° D、10°6. 把二次函数 化为 的形式是( )A、 B、 C、 D、7. 为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下.
A、30° B、25° C、15° D、10°6. 把二次函数 化为 的形式是( )A、 B、 C、 D、7. 为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下.身高
人数
60
260
550
130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于 的概率是( )
A、0.32 B、0.55 C、0.68 D、0.878. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BD交于点F,则S△DEF:S△ADF:S△ABF等于( )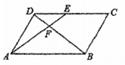 A、2:3:5 B、4:9:25 C、2:5:25 D、4:10:259. 设A(-1, )、B(1, )、C(3, )是抛物线 上的三个点,则 、 、 的大小关系是( )A、 < < B、 < < C、 < < D、 < <10. 如图,等边 的边长为 ,以O为圆心, 为直径的半圆经过点A,连接 , 相交于点P,将等边 从 与 重合的位置开始,绕着点O顺时针旋转 ,交点P运动的路径长是( )
A、2:3:5 B、4:9:25 C、2:5:25 D、4:10:259. 设A(-1, )、B(1, )、C(3, )是抛物线 上的三个点,则 、 、 的大小关系是( )A、 < < B、 < < C、 < < D、 < <10. 如图,等边 的边长为 ,以O为圆心, 为直径的半圆经过点A,连接 , 相交于点P,将等边 从 与 重合的位置开始,绕着点O顺时针旋转 ,交点P运动的路径长是( )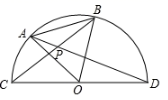 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,则 的值为.12. 如图,将△ABC绕顶点C逆时针旋转得到△A′B′C,且点B刚好落在A′B′上.若∠A=25°,∠BCA′=45°,则∠A′BA=度
 13. 现有A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x、小明 掷B立方体朝上的数字为y来确定点P( ),那么它们各掷一次所确定的点P落在已知抛物线 上的概率为.14. 如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= .
13. 现有A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x、小明 掷B立方体朝上的数字为y来确定点P( ),那么它们各掷一次所确定的点P落在已知抛物线 上的概率为.14. 如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= . 15. 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣2,4),B(1,1),则方程ax2=bx+c的解是 .
15. 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣2,4),B(1,1),则方程ax2=bx+c的解是 .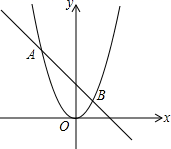 16. 如图,在正方形ABCD中,以CD为底边作等腰 ,使得点E在正方形ABCD内部,且 ,连接BD交CE于点F . 过点C作 于点G , 过点G作 于点H , 连接HF . 若 , ,则四边形AEFH的面积为 .
16. 如图,在正方形ABCD中,以CD为底边作等腰 ,使得点E在正方形ABCD内部,且 ,连接BD交CE于点F . 过点C作 于点G , 过点G作 于点H , 连接HF . 若 , ,则四边形AEFH的面积为 .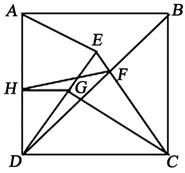
三、综合题
-
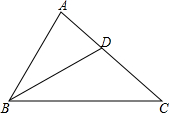
17. 如图,已知点D是 的边AC上的一点,连接 , , .
 (1)、求证: ∽ ;(2)、求线段CD的长.18. 小明和小亮玩一个游戏,游戏规则是:在三张完全相同的卡片上分别标记 、 、 三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则小明获胜,若抽出的两张卡片标记的数字之和为奇数,则小亮获胜.你认为这个游戏公平吗?请说明理由.19. 已知,如图所示,直线l经过点A(4,0)和B(0,4),它与抛物线y=ax2在第一象限内交于点P,又△AOP的面积为 ,求a的值.
(1)、求证: ∽ ;(2)、求线段CD的长.18. 小明和小亮玩一个游戏,游戏规则是:在三张完全相同的卡片上分别标记 、 、 三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则小明获胜,若抽出的两张卡片标记的数字之和为奇数,则小亮获胜.你认为这个游戏公平吗?请说明理由.19. 已知,如图所示,直线l经过点A(4,0)和B(0,4),它与抛物线y=ax2在第一象限内交于点P,又△AOP的面积为 ,求a的值.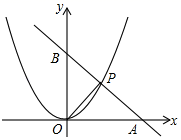 20. 如图,AB是⊙O的直径,点C,D在⊙O上,已知∠ABD=45°,BC=6,AC=8.
20. 如图,AB是⊙O的直径,点C,D在⊙O上,已知∠ABD=45°,BC=6,AC=8.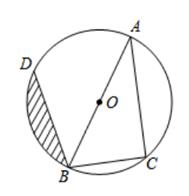 (1)、求BD的长;(2)、求图中阴影部分的面积.21. 如图1,已知正方形 和正方形 ,点 在同一直线上,连接 , , 与 相交于点 .
(1)、求BD的长;(2)、求图中阴影部分的面积.21. 如图1,已知正方形 和正方形 ,点 在同一直线上,连接 , , 与 相交于点 . (1)、求证: .(2)、如图2, 是 边上的一点,连接 交 于点 ,且 .
(1)、求证: .(2)、如图2, 是 边上的一点,连接 交 于点 ,且 .①求证: ;
②若 ,直接写出 的值.
22. 如图,二次函数y=-x²+(k-1)x+4的图像与y轴交与点A , 与x轴的负半轴交与点B , 且△AOB的面积为6.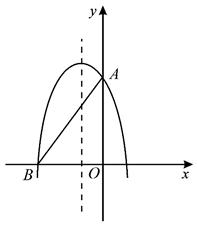 (1)、求A , B两点的坐标;(2)、求该二次函数的表达式;(3)、如果点p在坐标轴上,且△ABP是等腰三角形,求p的坐标.23. 如图1.已知⊙M与x轴交于A、B两点,与y轴交于C、D两点,A、B两点的横坐标分别为﹣1和7,弦AB的弦心距MN为3,
(1)、求A , B两点的坐标;(2)、求该二次函数的表达式;(3)、如果点p在坐标轴上,且△ABP是等腰三角形,求p的坐标.23. 如图1.已知⊙M与x轴交于A、B两点,与y轴交于C、D两点,A、B两点的横坐标分别为﹣1和7,弦AB的弦心距MN为3,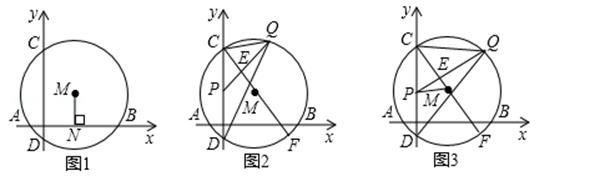 (1)、求⊙M的半径;(2)、求弦CD的长;(3)、如图2,P在弦CD上,且CP=2,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,求CQ的长;(4)、如图3.若P点是弦CD上一动点,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.
(1)、求⊙M的半径;(2)、求弦CD的长;(3)、如图2,P在弦CD上,且CP=2,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,求CQ的长;(4)、如图3.若P点是弦CD上一动点,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.