浙江省湖州市2021届九年级上学期数学期末模拟试卷
试卷更新日期:2021-01-05 类型:期末考试
一、单选题
-
1. 二次函数y=x2+2x-4的顶点坐标为( )A、(1,5) B、(-1,5) C、(-1,-5) D、(1 ,-5)2. 下列各组的四条线段成比例的是( )A、 ,3,2, , B、4,6,5,10 C、1,2, ,2 D、2,3,4,13. 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2 ,EM=5,则⊙O的半径为( )
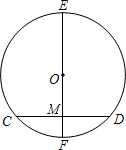 A、2 B、3 C、4 D、64. 在Rt 中,∠C=90°,如果AC=2, ,那么AB的长是( )A、 B、 C、 D、5. 如图,△ABC中,点D在边AB上,添加下列条件,不能判定△ACD∽△ABC的是( )
A、2 B、3 C、4 D、64. 在Rt 中,∠C=90°,如果AC=2, ,那么AB的长是( )A、 B、 C、 D、5. 如图,△ABC中,点D在边AB上,添加下列条件,不能判定△ACD∽△ABC的是( )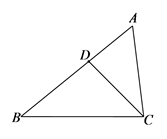 A、∠ACD=∠B B、∠ADC=∠ACB C、 D、AC2=AD·AB6. 现有三张正面分别标有数字 , , 的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n,则点 在第二象限的概率为( )A、 B、 C、 D、7. 如图, 和 是以点 为位似中心的位似三角形,若 为 的中点, ,则 的面积为( )
A、∠ACD=∠B B、∠ADC=∠ACB C、 D、AC2=AD·AB6. 现有三张正面分别标有数字 , , 的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n,则点 在第二象限的概率为( )A、 B、 C、 D、7. 如图, 和 是以点 为位似中心的位似三角形,若 为 的中点, ,则 的面积为( )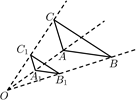 A、15 B、12 C、9 D、68. 如图,抛物线 的顶点为 ,与 轴的交点 在点 和 之间,下列结论正确的有( )
A、15 B、12 C、9 D、68. 如图,抛物线 的顶点为 ,与 轴的交点 在点 和 之间,下列结论正确的有( )① ;② ;③ ;④ .
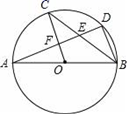
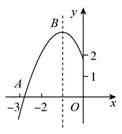 A、1个 B、2个 C、3个 D、4个9. 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
A、1个 B、2个 C、3个 D、4个9. 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
 A、②④⑤⑥ B、①③⑤⑥ C、②③④⑥ D、①③④⑤10. 如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O , 点P是BD上的一个动点,过点P作EF∥AC , 分别交正方形的两条边于点E , F , 连接OE , OF , 设BP=x , △OEF的面积为y , 则能大致反映y与x之间的函数关系的图像为( )
A、②④⑤⑥ B、①③⑤⑥ C、②③④⑥ D、①③④⑤10. 如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O , 点P是BD上的一个动点,过点P作EF∥AC , 分别交正方形的两条边于点E , F , 连接OE , OF , 设BP=x , △OEF的面积为y , 则能大致反映y与x之间的函数关系的图像为( )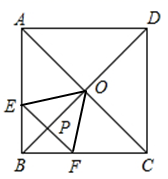 A、
A、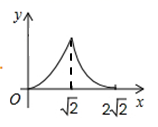 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 不透明袋子中装有12个球,其中有5个红球、4个绿球和3个蓝球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .12. 把抛物线 向左平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为.13. 在扇形OAB中,半径OA=2,S扇形OAB=π,则圆心角∠AOB=.
 14. 如图,在矩形ABCD中,E是边AB的中点,连结DE交对角线AC于点F.若AB=8,AD=6,则CF的长为 .
14. 如图,在矩形ABCD中,E是边AB的中点,连结DE交对角线AC于点F.若AB=8,AD=6,则CF的长为 .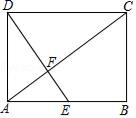 15. 如图,在 中, , , 的平分线与以 为直径的 交于点D,E为 的中点,则 .
15. 如图,在 中, , , 的平分线与以 为直径的 交于点D,E为 的中点,则 .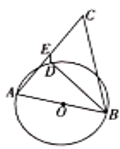 16. 对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是.
16. 对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是.三、综合题
-
17. 计算:18. 如图,在ΔABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
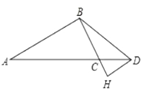 (1)、证明:ΔHCD∽ΔHDB.(2)、求DH的长度.19. 为贯彻落实全市城乡“清爽行动”暨生活垃圾分类攻坚大会精神,积极创建垃圾分类示范单位,我校举行了一次“垃圾分类”模拟活动. 我们将常见的生活垃圾分为四类:可回收垃圾、厨余垃圾、有害垃圾、其他垃圾,且应分别投放于4种不同颜色的对应垃圾桶中. 若在这次模拟活动中,某位同学将两种不同类型的垃圾先后随意投放于2种不同颜色的垃圾桶.(1)、请用列表或画树状图表示所有可能的结果数;(2)、求这位同学将两种不同类型的垃圾都正确投放的概率.20. 如图,山坡上有一棵与水平面垂 直的大树AB,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部B恰好落在山坡上的点D处,已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC= 38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m
(1)、证明:ΔHCD∽ΔHDB.(2)、求DH的长度.19. 为贯彻落实全市城乡“清爽行动”暨生活垃圾分类攻坚大会精神,积极创建垃圾分类示范单位,我校举行了一次“垃圾分类”模拟活动. 我们将常见的生活垃圾分为四类:可回收垃圾、厨余垃圾、有害垃圾、其他垃圾,且应分别投放于4种不同颜色的对应垃圾桶中. 若在这次模拟活动中,某位同学将两种不同类型的垃圾先后随意投放于2种不同颜色的垃圾桶.(1)、请用列表或画树状图表示所有可能的结果数;(2)、求这位同学将两种不同类型的垃圾都正确投放的概率.20. 如图,山坡上有一棵与水平面垂 直的大树AB,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部B恰好落在山坡上的点D处,已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC= 38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m (1)、求∠CAE的度数;(2)、求这棵大树折断前的高度;(结果保留整数,参考数据: ≈1.4, ≈1.7, ≈2.4)21. 如图,抛物线 与 轴交于 , 两点.与过B点的直线 y2=- x+b交于点C.
(1)、求∠CAE的度数;(2)、求这棵大树折断前的高度;(结果保留整数,参考数据: ≈1.4, ≈1.7, ≈2.4)21. 如图,抛物线 与 轴交于 , 两点.与过B点的直线 y2=- x+b交于点C.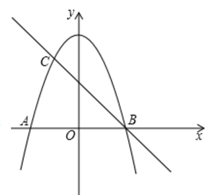 (1)、求直线 对应的函数解析式和点 的坐标;(2)、点 为抛物线上异于点 的一点,若 ,求点 的坐标.22. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?23. 如图,AB为☉O直径,半径为2,点D为弧 的中点,点C在☉O上由点A顺时针向点B运动(点C不与点A,点B重合),连接AC,BC,CD,AD,BD.
(1)、求直线 对应的函数解析式和点 的坐标;(2)、点 为抛物线上异于点 的一点,若 ,求点 的坐标.22. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?23. 如图,AB为☉O直径,半径为2,点D为弧 的中点,点C在☉O上由点A顺时针向点B运动(点C不与点A,点B重合),连接AC,BC,CD,AD,BD.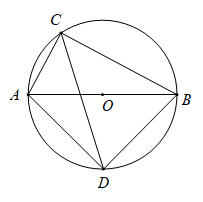 (1)、求证:CD是∠ACB的角平分线;(2)、求CD的长x的取值范围(直接写出答案)(3)、四边形ADBC的面积S是线段CD的长x的函数吗?如果是,求出函数解析式,并求出S的最大值,如果不是,请说明理由.24. 已知抛物线 ( 为正整数,且 )与 轴的交点为 和 , ,当 时,第 条抛物线 与 轴的交点为 和 ,其他依此类推.(1)、求 , 的值及抛物线 的解析式.(2)、抛物线 的顶点 的坐标为( , );依此类推,第 条抛物线 的顶点 的坐标为( , );所有抛物线的顶点坐标 满足的函数关系式是 .(3)、探究以下结论:
(1)、求证:CD是∠ACB的角平分线;(2)、求CD的长x的取值范围(直接写出答案)(3)、四边形ADBC的面积S是线段CD的长x的函数吗?如果是,求出函数解析式,并求出S的最大值,如果不是,请说明理由.24. 已知抛物线 ( 为正整数,且 )与 轴的交点为 和 , ,当 时,第 条抛物线 与 轴的交点为 和 ,其他依此类推.(1)、求 , 的值及抛物线 的解析式.(2)、抛物线 的顶点 的坐标为( , );依此类推,第 条抛物线 的顶点 的坐标为( , );所有抛物线的顶点坐标 满足的函数关系式是 .(3)、探究以下结论:①是否存在抛物线 ,使得 为等腰直角三角形?若存在,请求出抛物线 的解析式;若不存在,请说明理由.
②若直线 与抛物线 分别交于点 , , , ,则线段 , , , 的长有何规律?请用含有 的代数式表示.