浙江省金华市2021届九年级上学期数学期末模拟试卷
试卷更新日期:2021-01-05 类型:期末考试
一、单选题
-
1. 在下列二次函数中,其图象的对称轴为 的是( )A、 B、 C、 D、2. 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
 A、
A、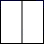 B、
B、 C、
C、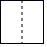 D、
D、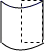 3. 下列一元二次方程中,没有实数根的是( ).A、 B、 C、 D、4. 如图,AB是⊙O的直径,C和D是⊙O上两点,连接AC,BC,BD,CD,若∠CDB=36°,则∠ABC=( )
3. 下列一元二次方程中,没有实数根的是( ).A、 B、 C、 D、4. 如图,AB是⊙O的直径,C和D是⊙O上两点,连接AC,BC,BD,CD,若∠CDB=36°,则∠ABC=( )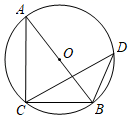 A、36° B、44° C、54° D、72°5. 为了解小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,9,7,26,17,9.这组数据的众数是( )A、17 B、7 C、16 D、156. 在扇形中,∠AOB=90°,面积为4πcm2 , 用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为 ( )A、1cm B、2cm C、 cm D、4cm7. 如图,在矩形ABCD中,对角线AC , BD交于点O , ,垂足为G , 延长GB至点E , 使得 ,连接OE交BC于点F.若 , ,则BF的长为( )
A、36° B、44° C、54° D、72°5. 为了解小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,9,7,26,17,9.这组数据的众数是( )A、17 B、7 C、16 D、156. 在扇形中,∠AOB=90°,面积为4πcm2 , 用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为 ( )A、1cm B、2cm C、 cm D、4cm7. 如图,在矩形ABCD中,对角线AC , BD交于点O , ,垂足为G , 延长GB至点E , 使得 ,连接OE交BC于点F.若 , ,则BF的长为( )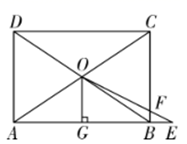 A、 B、1 C、 D、28. 抛物线 经过平移得到抛物线 ,平移过程正确的是( )A、先向下平移2个单位,再向左平移3个单位 B、先向上平移2个单位,再向右平移3个单位 C、先向下平移2个单位,再向右平移3个单位 D、先向上平移2个单位,再向左平移3个单位.9. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π10. 如图.抛物线y=ax2+bx+c(a≠0)经过点(-1,0),与y轴交于点(0,2),抛物线的对称轴为直线x=1,下列结论:①a+c=b:②方程ax2+bx+c=0的解为-1和3;③2a+b=0;④abc<0;其中正确的结论有( )
A、 B、1 C、 D、28. 抛物线 经过平移得到抛物线 ,平移过程正确的是( )A、先向下平移2个单位,再向左平移3个单位 B、先向上平移2个单位,再向右平移3个单位 C、先向下平移2个单位,再向右平移3个单位 D、先向上平移2个单位,再向左平移3个单位.9. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π10. 如图.抛物线y=ax2+bx+c(a≠0)经过点(-1,0),与y轴交于点(0,2),抛物线的对称轴为直线x=1,下列结论:①a+c=b:②方程ax2+bx+c=0的解为-1和3;③2a+b=0;④abc<0;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 使 在实数范围内有意义的x的取值范围是.12. 如图,已知△ABC∽△DBE,AB=6,DB=8,则 =.
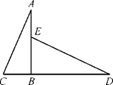 13. 已知反比例函数 ,当2≤x<5时,y的取值范围是.14. 如图.在边长为 的3×5正方形网格中,点A、B、C、D都在格点上,则 是 .
13. 已知反比例函数 ,当2≤x<5时,y的取值范围是.14. 如图.在边长为 的3×5正方形网格中,点A、B、C、D都在格点上,则 是 .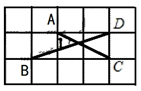 15. 如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为。
15. 如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为。 16. △ABC中,∠C=90°,∠A=20°,点O是AB的中点,将OB绕点O向三角形外部旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为。
16. △ABC中,∠C=90°,∠A=20°,点O是AB的中点,将OB绕点O向三角形外部旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为。三、综合题
-
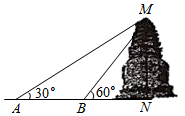
17. 计算: .18. 兰州白塔山山势起伏,山中白塔七级八面,上有绿项,下筑圆基,几经强烈地震仍屹立未动,显示了我国古代劳动人民在建筑艺术上的智慧与才能.
问题提出:如何测量白塔的高MN.
方案设计:九年级三班的白亮同学去测量白塔的高,如图,他在点A处测得塔尖M的仰角是30°,向前走了50米到达点B处,又测得塔尖M的仰角是60°.
问题解决:根据上述方案和数据,求白塔的高度MN(结果精确到1m,参考数据: ≈1.73).
 19. 一次函数 与反比例函数 交于点 A (1,3),B (3,m),
19. 一次函数 与反比例函数 交于点 A (1,3),B (3,m),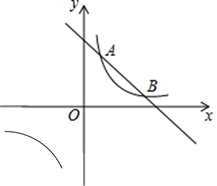 (1)、分别求两个函数的解析式;(2)、根据图像直接写出,当x为何值时, ;20. 随着疫情形势逐渐好转,各地企业陆续复工复产.为了促进员工进一步重视安全生产,掌握防疫知识,增强员工“科学防疫、安全生产”的意识,某企业在复工复产后组织开展了防疫安全知识竞赛活动.并随机抽取了部分员工的竞赛成绩(百分制)进行整理和分析(将分数分为四组:A. ,B. ,C. ,D. ,下面给出了部分信息:
(1)、分别求两个函数的解析式;(2)、根据图像直接写出,当x为何值时, ;20. 随着疫情形势逐渐好转,各地企业陆续复工复产.为了促进员工进一步重视安全生产,掌握防疫知识,增强员工“科学防疫、安全生产”的意识,某企业在复工复产后组织开展了防疫安全知识竞赛活动.并随机抽取了部分员工的竞赛成绩(百分制)进行整理和分析(将分数分为四组:A. ,B. ,C. ,D. ,下面给出了部分信息:
抽取的员工竞赛成绩分布表
组别
分数/分
频数
A
B
12
C
6
D
3
扇形统计图
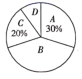
B组的成绩分别是88,86,80,86,84,82,80,86,82,84,88,86.(单位:分)
请解答下列问题:
(1)、 的值是 , B所占的百分比是 , B组数据的中位数是 .(2)、该企业共有320名员工参加了此次防疫安全知识竞赛活动,估计在本次活动中70分以下的人数.(3)、疫情期间,该企业的一些员工积极报名参加社区志愿者,挺身而出,服务于抗疫一线.为了进一步普及防疫知识,弘扬抗疫精神,该企业宣传部门打算从志愿者小王、小李、小张和小赵四人中随机抽取两人分享抗疫故事,请你用画树状图或列表的方法求出小王和小李被同时选中的概率.21. 如图,AB是⊙O的直径,点C是圆周上一点,连接AC、BC,以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P,使∠1=∠2=∠A.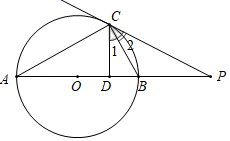 (1)、求证:直线PC是⊙O的切线;(2)、若CD=4,BD=2,求线段BP的长.22. 文具店新到一种计算器, 进价为25元,营销时发现:当销售单价定为30元时,每天的销售量为150件;
(1)、求证:直线PC是⊙O的切线;(2)、若CD=4,BD=2,求线段BP的长.22. 文具店新到一种计算器, 进价为25元,营销时发现:当销售单价定为30元时,每天的销售量为150件;若销售单价每上涨1元,每天的销售量就会减少10件。
(1)、写出商店销售这种计算器,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式:(2)、求销售单价定为多少元时,每天的销售利润最大?最大值是多少?(3)、商店的营销部结合上述情况,提出了A、B两种营销方案:方案A:为了让利学生,该计算器的销售利润不超过进价的24%;
方案B:为了满足市场需要,每天的销售量不少于120件。
请比较哪种方案的最大利润更高,并说明理由。
23. 如图,矩形 的两条边 , 的长是方程 的两根,其中 ,沿直线 将矩形折叠,使点 与 轴上的点 重合,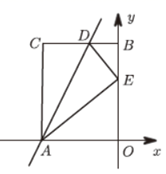 (1)、求 , 两点的坐标;(2)、求直线 的解析式;(3)、若点 在 轴上,平面内是否存在点 ,使以 , , , 为顶点的四边形为矩形?若存在,请直接写出点 的坐标;若不存在,请说明理由.24. 如图,抛物线C1的图象与x轴交A(−3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.
(1)、求 , 两点的坐标;(2)、求直线 的解析式;(3)、若点 在 轴上,平面内是否存在点 ,使以 , , , 为顶点的四边形为矩形?若存在,请直接写出点 的坐标;若不存在,请说明理由.24. 如图,抛物线C1的图象与x轴交A(−3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.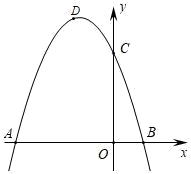
 (1)、求抛物线C1的解析式和D点坐标;(2)、将抛物线C1关于点B对称后的抛物线记为C2 , 点E为抛物线C2的顶点,求抛物线C2的解析式和E点坐标;(3)、是否在抛物线C2上存在一点P,在x轴上存在一点Q,使得以D,E,P,Q为顶点的四边形是平行四边形,若存在求出P点坐标,若不存在请说明理由.
(1)、求抛物线C1的解析式和D点坐标;(2)、将抛物线C1关于点B对称后的抛物线记为C2 , 点E为抛物线C2的顶点,求抛物线C2的解析式和E点坐标;(3)、是否在抛物线C2上存在一点P,在x轴上存在一点Q,使得以D,E,P,Q为顶点的四边形是平行四边形,若存在求出P点坐标,若不存在请说明理由.