浙江省丽水市2021届九年级上学期数学期末模拟试卷

试卷更新日期：2021-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中是随机事件的是（）

A、通常加热到100℃时，水沸腾 B、在只装有黑球和白球的袋子里，摸出红球 C、购买一张彩票，中奖 D、太阳从东方升起

查看试题解析
2. 下列说法正确的是（）

A、所有菱形都相似 B、所有矩形都相似 C、所有正方形都相似 D、所有平行四边形都相似

查看试题解析
3. 下列函数关系式中，属于二次函数的是（）

A、 $y = 2 x + 1$ B、 $y = x^{2} + \frac{1}{x}$ C、 $y = (x + 2) (x - 1) - x^{2}$ D、 $y = x^{2} - 1$

查看试题解析
4. 若α为锐角，且 $\sin (α - 10^{°}) = \frac{\sqrt{3}}{2}$ ，则α等于（）

A、80° B、70° C、60° D、50°

查看试题解析
5. 若一个圆内接正多边形的中心角是36°，则这个多边形是（）

A、正五边形 B、正八边形 C、正十边形 D、正十八边形

查看试题解析
6. 如图，点 $A$ 、 $B$ 、 $C$ 在 $⊙ O$ 上，若 $∠ B O C = 72 °$ ，则 $∠ B A C$ 的度数是（）

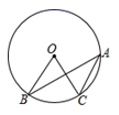A、18° B、36° C、54° D、72°

查看试题解析
7. 由 $y = x^{2}$ 平移得到抛物线 $y = {(x + 1)}^{2} - 2$ ，则下列平移过程正确的是（）

A、先向左平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向下平移2个单位 D、先向右平移1个单位，再向上平移2个单位

查看试题解析
8. 某校数学兴趣小组为测量学校旗杆AC的高度，在点F处竖立一根长为1.5米的标杆DF ，如图所示，量出DF的影子EF的长度为1米，再量出旗杆AC的影子BC的长度为6米，那么旗杆AC的高度为（）

A、6米 B、7米 C、8.5米 D、9米

查看试题解析
9. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是方程组 ${\begin{matrix} a x + b y = 1 \\ b x + a y = - 4 \end{matrix}$ 的解，则a+b的值是（）

A、﹣1 B、1 C、﹣5 D、5

查看试题解析
10. 在锐角三角形ABC中，AH是BC边上的高，分别以AB，AC为一边，向外作正方形ABDE和ACFG，连接CE，BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM=∠ABC，其中正确结论的个数是（）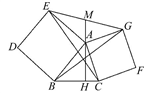

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 已知线段 $b$ 是线段 $a$ 、 $c$ 的比例中项，且 $a = 1 c m$ ， $c = 4 c m$ ，那么 $b =$ $c m$ .

查看试题解析
12. 圆心角为40°，半径为2的扇形的弧长为（结果保留π）.

查看试题解析

13. 表中记录了某种苹果树苗在一定条件下移植成活的情况：

移植的棵数n	200	500	800	2000	12000
成活的棵数m	187	446	730	1790	10836
成活的频率 $\frac{m}{n}$	0.935	0.892	0.913	0.895	0.903

由此估计这种苹果树苗移植成活的概率约为.（精确到0.1）

查看试题解析

14. 如图，在Rt△ACB中，∠ACB=90°，∠A=27°，将△ABC绕点C逆时针旋转α角到△A₁B₁C的位置，A₁B₁恰好经过点B，则旋转角α的度数是.

查看试题解析
15. 如图，一次函数 $y = k_{1} x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图像交于 $A$ 、 $B$ 两点，其横坐标分别为 $1$ 和 $5$ ，则关于 $x$ 的不等式 $k_{1} x + b - \frac{k_{2}}{x} < 0$ 的解集是．

查看试题解析
16. 如图，在△ABC中，M是AC中点，E是AB上一点，且AE= $\frac{1}{4}$ AB，连接EM并延长，交BC的延长线于点D，则 $\frac{B C}{C D}$ =。

查看试题解析

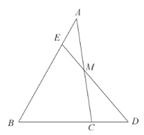
三、综合题

17.

(1)、解方程 $3 {(x - 2)}^{2} = 4 (x - 2)$ ；

(2)、已知 $a : b : c = 3 : 2 : 4$ .求 $\frac{a - 3 b + 4 c}{2 a + b - c}$ 的值.

查看试题解析
18. 如图，在△ABC中，BD⊥AC，AB＝6，AC＝5 $\sqrt{3}$ ，∠A＝30°.

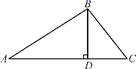(1)、求BD和AD的长；

(2)、求tanC的值.

查看试题解析
19. 如图，点E是正方形ABCD的边AB上一点，AB=4，DE=4.3，△DAE逆时针旋转后能够与△DCF重合.

(1)、旋转中心是，旋转角为 $°$ ；

(2)、请你判断△DFE的形状，简单说明理由；

(3)、四边形DEBF的面积为.

查看试题解析
20. 某校举行数学竞赛活动，晓晨和阿进两位同学得分相同，获并列第一名，于是每人可在准备好的2件奖品中获得其中一件，为了决定谁先选择奖品，并同时检验学生所学的数学知识，某位数学老师设计了一个趣味性游戏，游戏规则为：将如图1所示的四张扑克牌(方块2、黑桃4、黑桃5、梅花5)洗匀后，背面朝上放置在桌面上，晓晨从中随机抽取一张，记下牌面数字；如图2是一枚质地均匀的正方休骰子，六个面分别标有点数1，2，3，4，5，6，阿进掷一次骰子，记下骰子朝上一面的点数；若晓晨记下的牌面数字大于阿进记下骰子的点数，则晓晨先挑取奖品，否则，阿进先挑取奖品。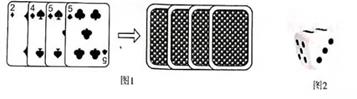

(1)、晓晨从四张扑克牌中随机抽取一张，牌面数字是5的概率是多少？

(2)、请用画树状图或列表的方法说明这个游戏对双方公平吗？

查看试题解析
21. 已知抛物线的顶点坐标是（2，-3），且经过点（1，-2.5）

(1)、求这个抛物线的函数表达式，并作出这个函数的大致图像.

(2)、当x在什么范围内时，y随x的增大而减小？

查看试题解析
22. 阅读下列解方程组的方法，然后解答问题：
解方程组 ${\begin{array}{l} 14 x + 15 y = 16 ① \\ 17 x + 18 y = 19 ② \end{array}$ 时，直接消元是很繁琐的，采用下面的解法则会简单许多.

解： $② - ①$ 得 $3 x + 3 y = 3$ ，所以 $x + y = 1$ .③

$③ \times 14$ ，得 $14 x + 14 y = 14$ .④

$① - ④$ ，得 $y = 2$ ，从而得 $x = - 1$ .

所以原方程组的解是 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ .

(1)、请你运用上述方法解方程组 ${\begin{array}{l} 2015 x + 2016 y = 2017 \\ 2018 x + 2019 y = 2020 \end{array}$ ，

(2)、猜测关于x，y的方程组 ${\begin{array}{l} m x + (m + 1) y = m + 2 \\ n x + (n + 1) y = n + 2 \end{array}$ ， $(m \neq n)$ 的解是什么？并用方程组的解加以验证.

查看试题解析
23. 如图，二次函数的图象与x轴相交于A(−3，0)、B(1，0)两点，与y轴相交于点C(0，3)，点C.D是二次函数图象上的一对对称点，一次函数的图象过点B，D.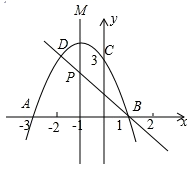

(1)、D点坐标；

(2)、求二次函数的解析式；

(3)、根据图象直接写出使一次函数值小于二次函数值的x的取值范围；

查看试题解析
24. 我们知道：有一内角为直角的三角形叫做直角三角形.类似地，我们定义：有一内角为45°的三角形叫做半直角三角形.如图，在平面直角坐标系中，O为原点，A（2，0），B（-2，0），D是y轴上的一个动点，∠ADC=90°（A、D、C按顺时针方向排列），BC与经过A、B、D三点的⊙M交于点E，DE平分∠ADC，连结AE，BD.显然△DCE、△DEF、△DAE是半直角三角形.

(1)、求证：△ABC是半直角三角形；

(2)、求证：∠DEC=∠DEA；

(3)、若点D的坐标为（0，8），求AE的长；

(4)、BC交y轴于点N，问 $\frac{C N}{O D}$ 的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由。

查看试题解析