浙江省宁波市2021届九年级上学期数学期末模拟试卷
试卷更新日期:2021-01-05 类型:期末考试
一、单选题
-
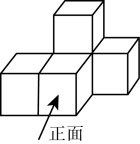
1. 如图,是由五个相同的小立方体搭成的几何体,这个几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在一个不透明的袋子中有3个白球、4个红球,这些球除颜色不同外其他完全相同。从袋子中随机摸出一个球, 它是红球的概率是( )A、 B、 C、 D、3. 如图,直线a//b//c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则DF的长是( ).
2. 在一个不透明的袋子中有3个白球、4个红球,这些球除颜色不同外其他完全相同。从袋子中随机摸出一个球, 它是红球的概率是( )A、 B、 C、 D、3. 如图,直线a//b//c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则DF的长是( ).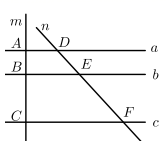 A、8 B、9 C、10 D、114. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )
A、8 B、9 C、10 D、114. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )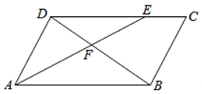 A、 B、 C、 D、5. 如图⊙O的直径 垂直于弦 ,垂足是 , , , 的长为( )
A、 B、 C、 D、5. 如图⊙O的直径 垂直于弦 ,垂足是 , , , 的长为( )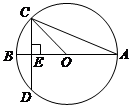 A、 B、4 C、 D、86. 已知 0≤x≤ , 那么函数 的最大值为( )A、0 B、 C、1 D、7. 如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
A、 B、4 C、 D、86. 已知 0≤x≤ , 那么函数 的最大值为( )A、0 B、 C、1 D、7. 如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.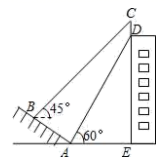 A、15-5 B、20-10 C、10-5 D、5 -58. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )
A、15-5 B、20-10 C、10-5 D、5 -58. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )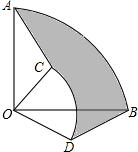 A、 B、
A、 B、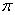 C、
C、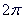 D、
D、 9. 如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF= AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( )
9. 如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF= AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( ) A、 B、 C、 D、110. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )
A、 B、 C、 D、110. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )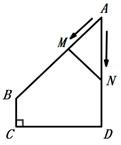 A、
A、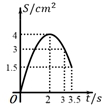 B、
B、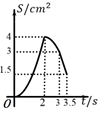 C、
C、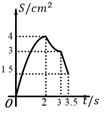 D、
D、
二、填空题
-
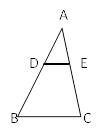
11. 已知∠A是锐角,且tanA= ,则sin = .12. 在一个不透明的布袋中,红色、黑色、白色的乒乓球共20个,除颜色,形状、大小质地等完全相同,小明通过多次摸球试验后发现其中摸到红色、黑色的频率稳定在5%和15%,则口袋中白色球的个数很可能是个.13. 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,如果AD=2cm,AB=6cm,AE=1.5cm,则EC=cm.
 14. 如图,⊙O的直径AB=2,C是半圆上任意一点,∠BCD=60°,则劣弧AD的长为。
14. 如图,⊙O的直径AB=2,C是半圆上任意一点,∠BCD=60°,则劣弧AD的长为。 15. 如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与射线PA相切时,圆心O平移的距离为.cm.
15. 如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与射线PA相切时,圆心O平移的距离为.cm.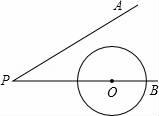 16. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .
16. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .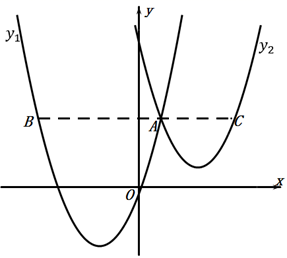
三、综合题
-
17. 线段 、 、 ,且 .(1)、求 的值.(2)、如线段 、 、 满足 ,求 的值.18. 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
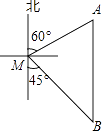 (1)、求渔船从B到A的航行过程中与码头M之间的最小距离.(2)、若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.19. 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且 ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)、求渔船从B到A的航行过程中与码头M之间的最小距离.(2)、若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.19. 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且 ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.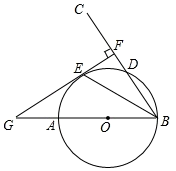 (1)、证明:GF是⊙O的切线;(2)、若AG=6,GE=6 ,求⊙O的半径.20. 在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下的三个小球中随机取出一个小球,记下数字为y,点Q坐标记作(x,y)。(1)、画树状图或列表,写出 Q点所有的坐标。(2)、计算由x、y确定的点Q (x,y)在函数y=-x+5图象上的概率;(3)、小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜。 这个游戏公平吗?说明理由;若不公平,怎么修改规则才对双方公平?21. 某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的50%.在销售过程中发现:当销售单价为35元时,每天可售出350件,若销售单价每提高5元,则每天销售量减少50件.设销售单价为x元(销售单价不低于35元).(1)、当这种儿童玩具以每件最高价出售时,每天的销售量为多少件?(2)、求这种儿童玩具每天获得的利润w(元)与销售单价x(元)之间的函数表达式;(3)、当销售单价为多少元时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少元?22. 据图回答问题
(1)、证明:GF是⊙O的切线;(2)、若AG=6,GE=6 ,求⊙O的半径.20. 在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下的三个小球中随机取出一个小球,记下数字为y,点Q坐标记作(x,y)。(1)、画树状图或列表,写出 Q点所有的坐标。(2)、计算由x、y确定的点Q (x,y)在函数y=-x+5图象上的概率;(3)、小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜。 这个游戏公平吗?说明理由;若不公平,怎么修改规则才对双方公平?21. 某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的50%.在销售过程中发现:当销售单价为35元时,每天可售出350件,若销售单价每提高5元,则每天销售量减少50件.设销售单价为x元(销售单价不低于35元).(1)、当这种儿童玩具以每件最高价出售时,每天的销售量为多少件?(2)、求这种儿童玩具每天获得的利润w(元)与销售单价x(元)之间的函数表达式;(3)、当销售单价为多少元时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少元?22. 据图回答问题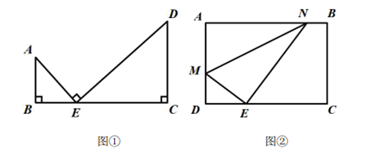 (1)、探究:如图①,点A、点 D在直线BC上方,且 AB⊥BC,DC⊥BC.点E是线段BC上的点,AE⊥DE.求证:△ABE∽△ECD.(2)、应用:如图①,在探究的条件下,若BE=2,CD=4,DE=6,求AE的长.(3)、拓展:如图②,矩形ABCD中,AB=12,BC=8.将矩形ABCD翻折,使点A落在边 CD上的点E处,折痕为MN.若DE= DC,则BN = .23. 已知:如图,AB是 的直径,点E为 上一点,点D是 上一点,连接 并延长至点C,使 与AE交于点F.
(1)、探究:如图①,点A、点 D在直线BC上方,且 AB⊥BC,DC⊥BC.点E是线段BC上的点,AE⊥DE.求证:△ABE∽△ECD.(2)、应用:如图①,在探究的条件下,若BE=2,CD=4,DE=6,求AE的长.(3)、拓展:如图②,矩形ABCD中,AB=12,BC=8.将矩形ABCD翻折,使点A落在边 CD上的点E处,折痕为MN.若DE= DC,则BN = .23. 已知:如图,AB是 的直径,点E为 上一点,点D是 上一点,连接 并延长至点C,使 与AE交于点F.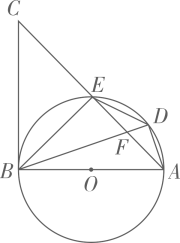 (1)、求证: 是 的切线;(2)、若 平分 ,求证: .24. 如图,抛物线 交x轴于A , B两点,交y轴于点C , 直线BC的表达式为y=-x+3.
(1)、求证: 是 的切线;(2)、若 平分 ,求证: .24. 如图,抛物线 交x轴于A , B两点,交y轴于点C , 直线BC的表达式为y=-x+3. (1)、求抛物线的表达式;(2)、动点D在直线BC上方的二次函数图象上,连接DC , DB , 设△BCD的面积为S , 求S的最大值;(3)、当点D为抛物线的顶点时,在坐标轴上是否存在一点Q , 使得以A , C , Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、动点D在直线BC上方的二次函数图象上,连接DC , DB , 设△BCD的面积为S , 求S的最大值;(3)、当点D为抛物线的顶点时,在坐标轴上是否存在一点Q , 使得以A , C , Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.