安徽省名校2020-2021学年高二上学期理数期中联考试卷
试卷更新日期:2021-01-04 类型:期中考试
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 直线的倾斜角是( )
A、 B、 C、 D、3. 已知空间中 , 是两条不同直线, 是平面,则( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则4. 下列函数既是奇函数又是增函数的是( )A、 B、 C、 D、5. 设 ,则 的大小关系为( )A、 B、 C、 D、6. 已知直线 过圆 的圆心,且与直线 平行,则 的方程是( )A、 B、 C、 D、7. 函数 在 的图像大致为( )A、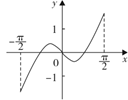 B、
B、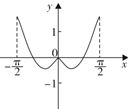 C、
C、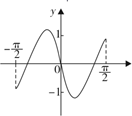 D、
D、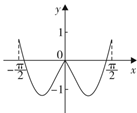 8. 已知 ,则 的值是( )A、 B、 C、 D、9. 已知数列 中, , ,则 等于( )A、 B、 C、 D、10. 中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式: .它表示:在受噪声干扰的信道中,最大信息传递速度 取决于信道带宽 ,信道内信号的平均功率 ,信道内部的高斯噪声功率 的大小,其中 叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,若不改变带宽 ,而将信噪比 从1000提升至4000,则 大约增加了( )附:A、10% B、20% C、50% D、100%11. 设 分别是 的内角A,B,C的对边,已知D是BC边的中点,且 ,则 等于( )A、 B、 C、 D、12. 设 , ,若函数 在 内有4个零点,则实数 的取值范围是( )A、 B、 C、 D、
8. 已知 ,则 的值是( )A、 B、 C、 D、9. 已知数列 中, , ,则 等于( )A、 B、 C、 D、10. 中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式: .它表示:在受噪声干扰的信道中,最大信息传递速度 取决于信道带宽 ,信道内信号的平均功率 ,信道内部的高斯噪声功率 的大小,其中 叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,若不改变带宽 ,而将信噪比 从1000提升至4000,则 大约增加了( )附:A、10% B、20% C、50% D、100%11. 设 分别是 的内角A,B,C的对边,已知D是BC边的中点,且 ,则 等于( )A、 B、 C、 D、12. 设 , ,若函数 在 内有4个零点,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 设 ,则 .14. 若变量 , 满足约束条件 ,则 的最小值为.15. 已知 , ,且 ,若 恒成立,则实数m的取值范围是 .16. 已知三棱锥 的各顶点都在同一球面上,且 平面 ,若该棱锥的体积为 , , , ,则此球的表面积= .
三、解答题
-
17. 已知等差数列 的前 项和为 ,等比数列 的前 项和为 .若 , , .(1)、求数列 与 的通项公式;(2)、求数列 的前 项和.18. 已知点 , , 为坐标原点,函数 .(1)、求函数 的解析式及最小正周期;(2)、若 为 的内角, , , 的面积为 ,求 的周长.19. 如图,在四棱锥 中,底面 是平行四边形, ,侧面 底面 , , .
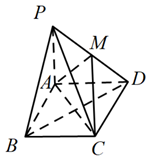 (1)、求证: 平面 ;(2)、过 的平面交 于点 ,若 ,求三棱锥 的体积.20. 如图, , 是某景区的两条道路(宽度忽略不计, 为东西方向),Q为景区内一景点,A为道路 上一游客休息区,已知 , (百米),Q到直线 , 的距离分别为3(百米), (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路 于点B,并在B处修建一游客休息区.
(1)、求证: 平面 ;(2)、过 的平面交 于点 ,若 ,求三棱锥 的体积.20. 如图, , 是某景区的两条道路(宽度忽略不计, 为东西方向),Q为景区内一景点,A为道路 上一游客休息区,已知 , (百米),Q到直线 , 的距离分别为3(百米), (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路 于点B,并在B处修建一游客休息区. (1)、求有轨观光直路 的长;(2)、已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时, (百米)( , ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道 以 (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(1)、求有轨观光直路 的长;(2)、已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时, (百米)( , ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道 以 (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.