广东省肇庆市怀集县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-01-04 类型：期中考试

进入出卷网下载

一、单选题

1. 方程 $x^{2} + x - 12 = 0$ 的两个根为（）

A、 $x_{1} = - 2, x_{2} = 6$ B、 $x_{1} = - 6, x_{2} = 2$ C、 $x_{1} = - 3, x_{2} = 4$ D、 $x_{1} = - 4, x_{2} = 3$

查看试题解析
2. 一元二次方程3x²+2x-5=0的常数项是（）

A、3 B、2 C、-5 D、5

查看试题解析
3. 二次函数y＝﹣2(x﹣1)²+3的最大值是（）.

A、﹣2 B、1 C、3 D、﹣1

查看试题解析
4. 一元二次方程2x²﹣7x﹣1＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
5. 下列方程中，关于x的一元二次方程是（）

A、（x+1）²=2（x+1） B、 $\frac{1}{x^{2}} + \frac{1}{x} - 2 = 0$ C、ax²+bx+c=0 D、x²+2x=x²﹣1

查看试题解析
6. 已知点（－1，2）在二次函数y=ax²的图象上，那么a的值是（）

A、1 B、2 C、 $\frac{1}{2}$ D、－ $\frac{1}{2}$

查看试题解析
7. 对于抛物线 $y = - \frac{1}{3} {(x - 5)}^{2} + 3$ ，下列说法正确的是（）

A、开口向下，顶点坐标 $(5 ， 3)$ B、开口向上，顶点坐标 $(5 ， 3)$ C、开口向下，顶点坐标 $(- 5 ， 3)$ D、开口向上，顶点坐标 $(- 5 ， 3)$

查看试题解析
8. 如图，在长为100 m，宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644m² ，则道路的宽应为多少米？设道路的宽为x m，则可列方程为（）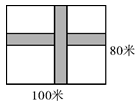

A、100×80－100x－80x=7644 B、(100－x)(80－x)＋x²=7644 C、(100－x)(80－x)=7644 D、100x＋80x－x²=7644

查看试题解析
9. 在同一坐标系中，二次函数 $y = a x^{2} + b x$ 与一次函数 $y = b x - a$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，一次函数 $y_{1} = - x$ 与二次函数为 $y_{2} = a x^{2} + b x + c$ 的图象相交于点M，N，则关于x的一元二次方程 $a x^{2} + (b + 1) x + c = 0$ 的根的情况是（）

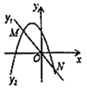A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有两个实数根

查看试题解析

二、填空题

11. 若 $y = (2 - m) x^{m^{2} - 2}$ 是二次函数，则m= ．

查看试题解析
12. 已知方程 $x^{2} - 4 x + 1 = 0$ 的两个实数根是 $x_{1} 、 x_{2}$ ，那么 $x_{1} + x_{2} =$ ．

查看试题解析
13. 抛物线y=x²﹣4x﹣1的对称轴为．

查看试题解析
14. 二次函数y=﹣2x²﹣x+3的图象与y轴的交点坐标为

查看试题解析
15. 若一个数的平方等于这个数的3倍，则这个数为．

查看试题解析
16. 抛物线 $y = {(x - 1)}^{2} + 2$ 向右平移 $2$ 个单位，再向上平移 $3$ 个单位，得到新的抛物线解析式是．

查看试题解析
17. 如图，在平面直角坐标系中，线段AB的两个端点的坐标分别为（-1，2）、（1，1）．抛物线y=ax²+bx+c（a≠0）与x轴交于C、D两点，点C在点D左侧，当顶点在线段AB上移动时，点C横坐标的最小值为-2．在抛物线移动过程中，a-b+c的最小值是．

查看试题解析

三、解答题

18. 解方程

(1)、 $x^{2} - 6 x = - 5$ ；

(2)、 ${(x + 4)}^{2} = 2 x + 8$ ．

查看试题解析
19. 已知二次函数的图象经过点 $(- 1 ， - 8)$ ，顶点为 $(2 ， 1)$ ．求这个二次函数的解析式．

查看试题解析
20. 已知：3是方程x²-2x+c=0的一个根，求方程的另一个根及c的值.

查看试题解析
21. 已知：二次函数 $y = - x^{2} + 2 x + 3$ ．

(1)、将函数关系式化为 $y = a {(x - h)}^{2} + k$ 的形式，并指出函数图象的对称轴和顶点坐标；

(2)、画出所给函数的图象．

查看试题解析
22. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析
23. 已知 $x_{1}$ 、 $x_{2}$ 是关于x的一元二次方程 $x^{2} - 2 (n + 1) x + n^{2} + 5 = 0$ 的两实数根．

(1)、若 $(x_{1} - 1) (x_{2} - 1) = 28$ ，求n的值；

(2)、已知等腰三角形 $A B C$ 的一边长为7，若 $x_{1}$ 、 $x_{2}$ 恰好是△ $A B C$ 另外两边的长，求这个三角形的周长．

查看试题解析
24. 随着互联网的普及，某手机厂商采用先网络预定，然后根据订单量生产手机的方式销售，2015年该厂商将推出一款新手机，根据相关统计数据预测，定价为2200元，日预订量为20000台，若定价每减少100元，则日预订量增加10000台．

(1)、设定价减少x元，预订量为y台，写出y与x的函数关系式；

(2)、若每台手机的成本是1200元，求所获的利润w（元）与x（元）的函数关系式，并说明当定价为多少时所获利润最大；

(3)、若手机加工厂每天最多加工50000台，且每批手机会有5%的故障率，通过计算说明每天最多接受的预订量为多少？按最大量接受预订时，每台售价多少元？

查看试题解析
25. 如图，在平面直角坐标系xOy中，二次函数y＝﹣ $\frac{1}{2}$ x²+bx+c的图象经过点A（4，0），C（0，2）．

(1)、求抛物线的表达式；

(2)、如图1，点E是第一象限的抛物线上的一个动点．当△ACE面积最大时，请求出点E的坐标；

(3)、如图2，在抛物线上是否存在一点P ，使∠CAP＝45°？若存在，求点P的坐标；若不存在，请说明理由．

查看试题解析