广东省韶关市新丰县2020-2021学年九年级上学期数学第二次月考试卷
试卷更新日期:2021-01-04 类型:月考试卷
一、单选题
-
1. 下列几何图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、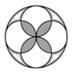 C、
C、 D、
D、 2. 一元二次方程x2+3x-1=0的解的情况是( )A、无解 B、有两个不相等的实数根 C、有两个相等的实数根 D、只有一个解3. 如图,在 中, ,将 绕点 逆时针旋转 角到 的位置,这时点 恰好落在边 的中点,则旋转角 的度数为( ).
2. 一元二次方程x2+3x-1=0的解的情况是( )A、无解 B、有两个不相等的实数根 C、有两个相等的实数根 D、只有一个解3. 如图,在 中, ,将 绕点 逆时针旋转 角到 的位置,这时点 恰好落在边 的中点,则旋转角 的度数为( ).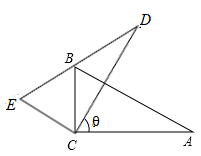 A、60° B、45° C、30° D、55°4. 已知 的半径为4cm,点A到圆心O的距离为3cm,则点 与 的位置关系是( ).A、点A在 内 B、点A在 上 C、点A在 外 D、不能确定5. 若x=1是关于x的方程 的一个根,则a的值为( )A、1 B、2 C、 D、6. 把函数 图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、7. 如图,四边形 是 的内接四边形, ,则 的度数为( )
A、60° B、45° C、30° D、55°4. 已知 的半径为4cm,点A到圆心O的距离为3cm,则点 与 的位置关系是( ).A、点A在 内 B、点A在 上 C、点A在 外 D、不能确定5. 若x=1是关于x的方程 的一个根,则a的值为( )A、1 B、2 C、 D、6. 把函数 图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、7. 如图,四边形 是 的内接四边形, ,则 的度数为( )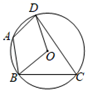 A、 B、 C、 D、8. 对于二次函数 的图象,下列说法正确的是( )A、开口向下; B、对称轴是直线x=-1; C、顶点坐标是(-1,2); D、与x轴没有交点.9. 如图,在宽为22m、长为30m的矩形地面上修建两条宽度相同的道路,余下部分作为耕地,若耕地面积需要560m2 , 则修建的路宽应为( )
A、 B、 C、 D、8. 对于二次函数 的图象,下列说法正确的是( )A、开口向下; B、对称轴是直线x=-1; C、顶点坐标是(-1,2); D、与x轴没有交点.9. 如图,在宽为22m、长为30m的矩形地面上修建两条宽度相同的道路,余下部分作为耕地,若耕地面积需要560m2 , 则修建的路宽应为( ) A、1m B、1.5m C、2 D、2.5m10. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
A、1m B、1.5m C、2 D、2.5m10. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )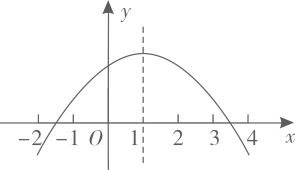 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 抛物线y=﹣x2开口向 .12. 在平面直角坐标系中,点(3,-4)关于原点对称的点的坐标是 .13. 如图,在 中,A,B,C是 上三点,如果 ,那么 的度数为.
 14. 抛物线 的顶点坐标是 .15. 抛物线 与 轴有两个交点,则原点左侧交点坐标为.16. 若a是方程x2﹣x﹣1=0的一个根,则a2﹣a+2017的值为 .17. 如图,点O是等边 内一点, ,将 绕点C按顺时针方向旋转 得 ,连接 ,若 ,则 的度数为 .
14. 抛物线 的顶点坐标是 .15. 抛物线 与 轴有两个交点,则原点左侧交点坐标为.16. 若a是方程x2﹣x﹣1=0的一个根,则a2﹣a+2017的值为 .17. 如图,点O是等边 内一点, ,将 绕点C按顺时针方向旋转 得 ,连接 ,若 ,则 的度数为 .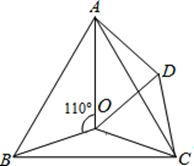
三、解答题
-
18. 解方程: .19. 如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50后得到△A′BC′.已知A′C′∥BC , 求∠A的度数.
 20. 已知关于x的一元二次方程 .(1)、如果此方程有两个相等的实数根,求n的值;(2)、如果此方程有一个实数根为0,求另外一个实数根.21. 如图,在边长为1个单位长度的小正方形组成的网格中, 的顶点均在格点上,点A的坐标为 ,点B的坐标为 ,点C的坐标为 .
20. 已知关于x的一元二次方程 .(1)、如果此方程有两个相等的实数根,求n的值;(2)、如果此方程有一个实数根为0,求另外一个实数根.21. 如图,在边长为1个单位长度的小正方形组成的网格中, 的顶点均在格点上,点A的坐标为 ,点B的坐标为 ,点C的坐标为 .
⑴以点C为旋转中心,将 旋转180°后得到 ,请画出 ;
⑵平移 ,使点A的对应点 的坐标为 ,请画出 .
⑶若将 绕点P旋转可得到 ,则点P的坐标为
22. 如图,AB是⊙O的一条弦,OD⊥AB于点C , 交⊙O于点D , 连接OA . 若AB=4,CD=1,求⊙O半径的长. 23. 随着全球疫情的爆发,医疗物资的极度匮乏,中国许多企业都积极的宣布生产医疗物资以应对疫情,某工厂及时引进了一条口罩生产线生产口罩,开工第一天生产256万个,第三天生产400万个,若每天增长的百分率相同.试回答下列问题:(1)、求每天增长的百分率;(2)、经调查发现,1条生产线最大产能是1000万个 天,若每增加1条生产线,每条生产线的最大产能将减少50万个 天,现该厂要保证每天生产口罩4000万件,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
23. 随着全球疫情的爆发,医疗物资的极度匮乏,中国许多企业都积极的宣布生产医疗物资以应对疫情,某工厂及时引进了一条口罩生产线生产口罩,开工第一天生产256万个,第三天生产400万个,若每天增长的百分率相同.试回答下列问题:(1)、求每天增长的百分率;(2)、经调查发现,1条生产线最大产能是1000万个 天,若每增加1条生产线,每条生产线的最大产能将减少50万个 天,现该厂要保证每天生产口罩4000万件,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?

