广东省佛山市四校联考2020-2021学年九年级上学期数学第二次月考试卷

试卷更新日期：2021-01-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 计算 $\sin 30 °$ 的值等于（）

A、 $\sqrt{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2.
如图所示几何体的俯视图是（　　）

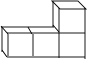A、 B、 C、 D、

查看试题解析
3. 菱形具有而矩形不一定具有的性质是（）

A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、四条边相等

查看试题解析
4. 一元二次方程 $x^{2} + x + \frac{1}{3} = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
5. 下列说法正确的是（）

A、为了解一批灯泡的使用寿命，应采用普查的方式 B、抛掷两枚质量均匀的硬币，出现两面都是正面的概率为 $\frac{1}{3}$ C、某种彩票中奖的概率是 $\frac{1}{1000}$ ，买1000张这种彩票一定会中奖1000 D、在一定条件下大量重复试验时，某个事件发生的频率稳定在0.6附近摆动，估计该事件发生的概率为0.6

查看试题解析
6. 如图是小红在某天四个时刻看到一根木棒及其影子的情况，那么她看到的先后顺序是（）

A、①②③④ B、④③①② C、④①③② D、②①③④

查看试题解析
7. 如图，在 $△ A B C$ 中，点D、E分别在 $A B$ 、 $A C$ 边上， $D E // B C$ ，若 $\frac{A D}{B D} = 4$ ， $D E = 8$ ，则 $B C$ 等于（）

A、10 B、12 C、16 D、20

查看试题解析
8. 某口罩加工厂今年一月口罩产值达80万元，第一季度总产值达340万元，问二、三月份的月平均增长率是多少？设月平均增长率为x，则根据题意可得方程为（）

A、 $80 {(1 + x)}^{2} = 340$ B、 $80 + 80 (1 + x) + 80 (1 + 2 x) = 340$ C、 $80 {(1 + x)}^{3} = 340$ D、 $80 + 80 (1 + x) + 80 {(1 + x)}^{2} = 340$

查看试题解析
9. 函数 $y = k x + k$ 与 $y = \frac{k}{x}$ （ $k \neq 0$ ）在同一平面直角坐标系的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，下列四个结论：
①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD= $\sqrt{2}$ .其中正确的结论有（）

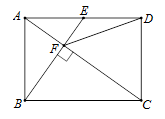A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 计算： $\sin 60 ° - \cos 30 ° + \tan 45 ° =$ ．

查看试题解析
12. 已知 $x = - 1$ 是一元二次方程 $a x^{2} - 3 x + 4 = 0$ （ $a \neq 0$ ）的一个根，则另一根是．

查看试题解析
13. 小明用这样的方法来测量某建筑物的高度：如图，在地面上放一面镜子，调整位置，直至刚好能从镜子中看到建筑物的顶端．如果此时小明与镜子的距离是2m，镜子与建筑物的距离是20m. 他的眼睛距地面1.5m，那么该建筑物的高是．

查看试题解析
14. 一个主持人站在舞台的黄金分割点处最自然得体，如果舞台 $A B$ 长为20米，一个主持人现在站在A处，则他应至少再走米才理想．（结果精确到0.1米）

查看试题解析
15. 有一个只放满形状大小都一样的白色小球的不透明盒子，小刚想知道盒内有多少白球，于是小刚向这个盒中放了8个黑球（黑球的形状大小与白球一样），摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，估计盒中大约有白球．

查看试题解析
16. 正方形 $A B C D$ 的边长为 $\sqrt{2}$ ，点P为对角线 $A C$ 上一个动点， $P E ⊥ A B$ ， $P F ⊥ C B$ ，垂足分别是E，F．当P在 $A C$ 上移动时，线段 $E F$ 的最小值是．

查看试题解析
17. 已知反比例函数 $y = \frac{8}{x}$ 和 $y = \frac{3}{x}$ 在第一象限内的图象如图所示，则 $△ A M N$ 的面积为．

查看试题解析

三、解答题

18. 解方程： $x (2 x + 1) = 2 x + 1$

查看试题解析
19. 已知： $△ A B C$ 三个顶点的坐标分别为 $A (- 2 ， - 2)$ ， $B (- 5 ， - 4)$ ， $C (- 1 ， - 5)$ ．

⑴画出将 $△ A B C$ 绕点A逆时针旋转 $90 °$ 的 $△ A B_{1} C_{1}$ ；

⑵以点O为位似中心，将 $△ A B C$ 放大为原来的2倍，得到 $△ A_{2} B_{2} C_{2}$ ，请在网格纸中画出 $△ A_{2} B_{2} C_{2}$ ，并写出点 $C_{2}$ 的坐标．

⑶若图中每个小方格的面积为1，请直接写出 $△ A_{2} B_{2} C_{2}$ 的面积。

查看试题解析
20. 如图，在 $△ A B C$ 中， $\cos B = \frac{\sqrt{2}}{2}$ ， $\sin C = \frac{3}{5}$ ， $A C = 10$ ，求 $△ A B C$ 的面积．

查看试题解析
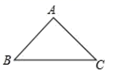21. 忻州有“秀容古城”之称，某校就同学们对“忻州历史文化”的了解程度进行随机抽样调查，将调查结果绘制成如下两幅统计图：

根据统计图的信息，解答下列问题：

(1)、本次共调查名学生，条形统计图中m=；

(2)、若该校共有学生1000名，则该校约有名学生不了解“忻州历史文化”；

(3)、调查结果中，该校八年级（2）班学生中了解程度为“很了解”的同学是两名男生、一名女生，现准备从其中随机抽取两人去市里参加“忻州历史文化”知识竞赛，用树状图或列表法，求恰好抽中一男生一女生的概率．

查看试题解析
22. “新冠”疫情蔓延全球，口罩成了人们的生活必需品，某药店销售普通口罩和N95口罩，今年3月份的进价如表：

普通口罩

N95口罩

进价（元/包）

8

20

(1)、计划N95口罩每包售价比普通口罩售价贵16元，7包普通口罩和3包N95口罩总售价相同，求每包普通口罩和N95口罩的售价；

(2)、按（1）中售价销售一段时间后，发现普通口罩的日均销售量为120包，当每包售价降价1元时，日均销售量增加20包，该药店秉承让利于民的原则，对普通口罩进行降价销售，但要保证当天的利润为320元，求此时普通口罩每包售价．

查看试题解析
23. 已知：如图，在平行四边形ABCD中，对角线AC与BD交于点O ，点E是DB延长线上的一点，且EA＝EC ，分别延长AD、EC交于点F ．

(1)、求证：四边形ABCD为菱形；

(2)、如果∠AEC＝2∠BAC ，求证：EC•CF＝AF•AD ．

查看试题解析
24. 如图，一次函数 $y_{1} = k_{1} x + 2$ 与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象交于点 $A (4 ， m)$ 和 $B (- 8 ， - 2)$ ，与y轴交于点C.

(1)、 $k_{1}$ = ， $k_{2}$ =；

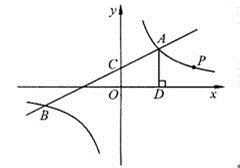(2)、根据函数图象可知，当 $y_{1}$ ＞ $y_{2}$ 时，x的取值范围是；

(3)、过点A作AD⊥x轴于点D ，点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E ，当 $S_{四边形 O D A C}$ ： $S_{△ O D E}$ =3：1时，求点P的坐标.

查看试题解析
25. 已知：如图，正方形 $A B C D$ 的边长为1，动点E、F分别在边 $A B$ 、对角线 $B D$ 上（点F与点D、B都不重合）且 $A E = \sqrt{2} D F$ ．

(1)、设 $D F = x$ ， $C F^{2} = y$ ，求：y与x的函数关系式，并直接写出自变量x的取值范围；

(2)、求证： $F C = F E$ ；

(3)、是否存在以线段 $A E$ 、 $D F$ 、 $C F$ 的长为边的直角三角形？若存在，请求出x的值；若不存在，请说明理由．

查看试题解析

	普通口罩	N95口罩
进价（元/包）	8	20