人教版数学九年级下册 第二十七章 相似 27.2.1 相似三角形的判定 同步练习
试卷更新日期:2021-01-02 类型:同步测试
一、单选题
-
1. 如图,在 中, , , ,将 沿图示中的虚线 剪开,剪下的三角形与原三角形不相似的是( )
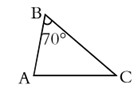 A、
A、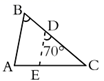 B、
B、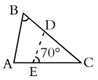 C、
C、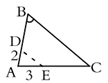 D、
D、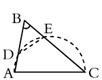 2. 下列各组长度的线段(单位: )中,成比例线段的是( )A、1,2,3,4 B、1,2,3,5 C、2,3,4,5 D、2,3,4,63. 已知四条线段a,b,c,d是成比例线段,即 = ,下列说法错误的是( )A、ad=bc B、 = C、 = D、 =4. 下列判断中,错误的有( )A、三边对应成比例的两个三角形相似 B、两边对应成比例,且有一个角相等的两个三角形相似 C、有一个锐角相等的两个直角三角形相似 D、有一个角是100°的两个等腰三角形相似5. 如图,在△ABC中,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为( )
2. 下列各组长度的线段(单位: )中,成比例线段的是( )A、1,2,3,4 B、1,2,3,5 C、2,3,4,5 D、2,3,4,63. 已知四条线段a,b,c,d是成比例线段,即 = ,下列说法错误的是( )A、ad=bc B、 = C、 = D、 =4. 下列判断中,错误的有( )A、三边对应成比例的两个三角形相似 B、两边对应成比例,且有一个角相等的两个三角形相似 C、有一个锐角相等的两个直角三角形相似 D、有一个角是100°的两个等腰三角形相似5. 如图,在△ABC中,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为( )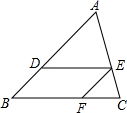 A、6 B、8 C、10 D、126. 下列条件中,不能判断△ABC与△DEF相似的是( )A、∠A=∠D , ∠B=∠F B、 且∠B=∠D C、 D、 且∠A=∠D7. 如图所示,在▱ABCD.BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A、6 B、8 C、10 D、126. 下列条件中,不能判断△ABC与△DEF相似的是( )A、∠A=∠D , ∠B=∠F B、 且∠B=∠D C、 D、 且∠A=∠D7. 如图所示,在▱ABCD.BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )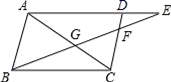 A、3对 B、4对 C、5对 D、6对8. 如图,下列条件中不能判定△ACD∽△ABC的是( )
A、3对 B、4对 C、5对 D、6对8. 如图,下列条件中不能判定△ACD∽△ABC的是( )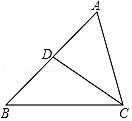 A、∠ADC=∠ACB B、 C、∠ACD=∠B D、AC2=AD•AB9. 如图,AG:GD=4:1,BD:DC=2:3,则 AE:EC 的值是( )
A、∠ADC=∠ACB B、 C、∠ACD=∠B D、AC2=AD•AB9. 如图,AG:GD=4:1,BD:DC=2:3,则 AE:EC 的值是( )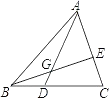 A、3:2 B、4:3 C、6:5 D、8:5
A、3:2 B、4:3 C、6:5 D、8:5二、填空题
-
10. 如图,在△ABC中,D , E两点分别在AB , AC边上,DE∥BC.如果 ,AC=10,那么EC= .
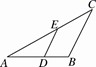 11. 如图,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,点P从点B出发,沿BC以2 cm/s的速度向点C移动,点Q从点C出发,以1 cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=时,△CPQ与△CBA相似.
11. 如图,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,点P从点B出发,沿BC以2 cm/s的速度向点C移动,点Q从点C出发,以1 cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=时,△CPQ与△CBA相似.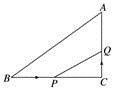 12. 的边长分别为 的边长分别 ,则 与 (选填“一定”“不一定” “一定不”)相似13. 如图所示,在△ABC中,已知BD=2DC,AM=3MD,过M作直线交AB,AC于P,Q两点.则 = .
12. 的边长分别为 的边长分别 ,则 与 (选填“一定”“不一定” “一定不”)相似13. 如图所示,在△ABC中,已知BD=2DC,AM=3MD,过M作直线交AB,AC于P,Q两点.则 = .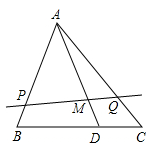
三、解答题
-
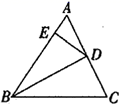
14. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.
证明:△BCD∽△BDE.
 15. 如图,直线 ,直线 相交于点 ,且分别与直线 相交于点 和点 ,已知 , , , ,求 的长度.
15. 如图,直线 ,直线 相交于点 ,且分别与直线 相交于点 和点 ,已知 , , , ,求 的长度.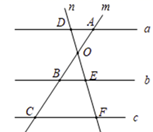 16. 已知:如图, 中,点 分别在边 上,且 与 交于点 与 交于点 .求证:点 是线段 的中点.
16. 已知:如图, 中,点 分别在边 上,且 与 交于点 与 交于点 .求证:点 是线段 的中点.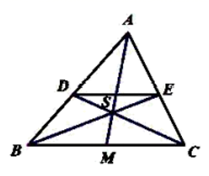 17. 如图,把一块直角三角板的直角顶点P放在正方形ABCD的边BC上,并且使一条直角边经过点D,另一条直角边与AB交于点Q,请写出一对相似三角形,并加以证明(图中不添加字幕和线段)
17. 如图,把一块直角三角板的直角顶点P放在正方形ABCD的边BC上,并且使一条直角边经过点D,另一条直角边与AB交于点Q,请写出一对相似三角形,并加以证明(图中不添加字幕和线段)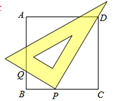
四、综合题
-
18. 如图1,在正方形ABCD中,E是边BC上的点,将线段DE绕点E逆时针旋转90°得到EF,过点C作CG∥EF交BA(或其延长线)于点G,连接DF,FG.
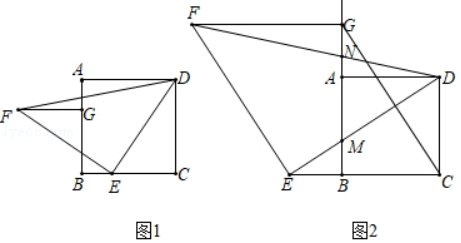 (1)、FG与CE的数量关系是 , 位置关系是.(2)、如图2,若点E是CB延长线上的点,其它条件不变.
(1)、FG与CE的数量关系是 , 位置关系是.(2)、如图2,若点E是CB延长线上的点,其它条件不变.①(1)中的结论是否仍然成立?请作出判断,并给予证明;
②DE,DF分别交BG于点M,N,若BC=2BE,求 .