人教版数学九年级下册 第二十七章 相似 27.3 位似 同步练习
试卷更新日期:2021-01-02 类型:同步测试
一、单选题
-
1. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣2,1)或(2,﹣1) D、(﹣8,4)或(8,﹣4)2. 下列相似图形不是位似图形的是( )A、
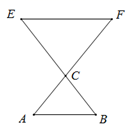 B、
B、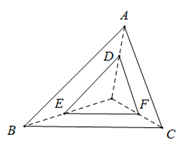 C、
C、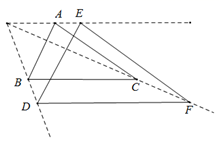 D、
D、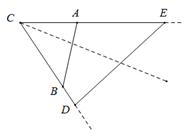 3. 已知 ,任取一点 ,连接AO , BO , CO , 并取它们的中点D , E , F , 得 ,则下列说法正确的个数是( )
3. 已知 ,任取一点 ,连接AO , BO , CO , 并取它们的中点D , E , F , 得 ,则下列说法正确的个数是( )① 与 是位似图形;② 与 是相似图形;③ 与 的周长比为 ;④ 与 的面积比为 .
A、1 B、2 C、3 D、44.观察下图,在下列四种图形变换中,该图案不包含的变换是( )
 A、平移 B、轴对称 C、旋转 D、位似5. 如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点
A、平移 B、轴对称 C、旋转 D、位似5. 如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点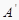 ,
, 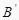 ,
, 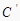 .下列说法正确的是( )
.下列说法正确的是( ) 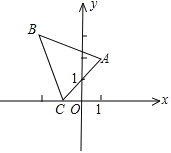 A、△
A、△ 与△ABC是位似图形,位似中心是点(1,0)
B、△
与△ABC是位似图形,位似中心是点(1,0)
B、△  与△ABC是位似图形,位似中心是点(0,0)
C、△
与△ABC是位似图形,位似中心是点(0,0)
C、△  与△ABC是相似图形,但不是位似图形
D、△
与△ABC是相似图形,但不是位似图形
D、△  与△ABC不是相似图形
与△ABC不是相似图形
二、填空题
-
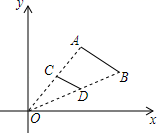
6. 如图,已知线段AB两个端点的坐标分别为A(4,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD , 则端点D坐标为 .
 7. 在平面直角坐标系中,将 以点 为位似中心, 为位似比作位似变换,得到 .已知 ,则点 的坐标是 .
7. 在平面直角坐标系中,将 以点 为位似中心, 为位似比作位似变换,得到 .已知 ,则点 的坐标是 . 8. 在平面直角坐标系中,点A的坐标是 ,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数的解析式为 .9. 已知:如图, , ,以原点O为位似中心,相似比 ,把 在点O另一侧缩小,则点E的对应点 的坐标为 .
8. 在平面直角坐标系中,点A的坐标是 ,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数的解析式为 .9. 已知:如图, , ,以原点O为位似中心,相似比 ,把 在点O另一侧缩小,则点E的对应点 的坐标为 .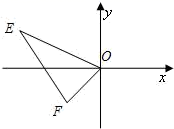 10. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A , B , E在x轴上,若正方形BEFG的边长为6,则C点坐标为 .
10. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A , B , E在x轴上,若正方形BEFG的边长为6,则C点坐标为 .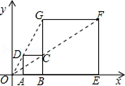 11. 如图,平面直角坐标系中有正方形 和正方形 ,若点 和点 的坐标分别为 , ,则两个正方形的位似中心的坐标是 .
11. 如图,平面直角坐标系中有正方形 和正方形 ,若点 和点 的坐标分别为 , ,则两个正方形的位似中心的坐标是 .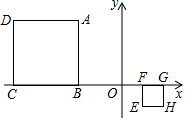
三、作图题
-
12. 如图,已知△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3)、
B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
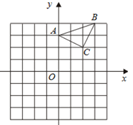 (1)、画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是(2)、以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1(3)、求四边形 的面积.13. 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)、画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是(2)、以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1(3)、求四边形 的面积.13. 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.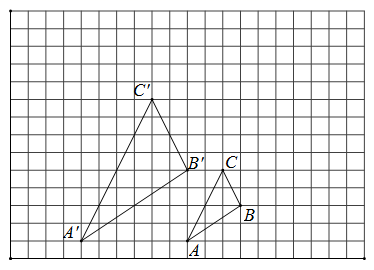 (1)、画出位似中心O;(2)、求出△ABC与△A′B′C′的相似比.14. 如图,在 网格图中,每个小正方形边长均为 ,点 和四边形 的顶点均在小正方形的顶点上.
(1)、画出位似中心O;(2)、求出△ABC与△A′B′C′的相似比.14. 如图,在 网格图中,每个小正方形边长均为 ,点 和四边形 的顶点均在小正方形的顶点上.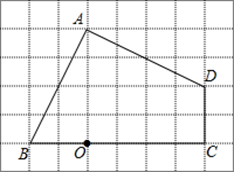 (1)、以 为位似中心,在网格图中作四边形 和四边形 位似,且位似比为 ;(2)、根据(1)填空: .
(1)、以 为位似中心,在网格图中作四边形 和四边形 位似,且位似比为 ;(2)、根据(1)填空: .四、综合题
-
15. 请阅读下列材料,并完成相应的任务:
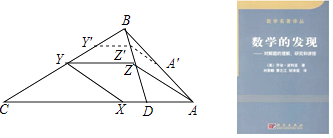
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴ .
同理可得 .∴ .
∵Z'A'=Y'Z',∴ZA=YZ.
任务:
(1)、请根据上面的操作步骤及部分证明过程,判断四边形AXYZ的形状,并加以证明;(2)、请再仔细阅读上面的操作步骤,在(1)的基础上完成AX=BY=XY的证明过程;(3)、上述解决问题的过程中,通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,这里运用了下面一种图形的变化是 .A、平移 B、旋转 C、轴对称 D、位似16. (1)在正方形方格纸中,我们把顶点均在“格点”上的三角形称为“格点三角形”,如图△ABC是一个格点三角形,点A的坐标为(-2,2). (1)、点B的坐标为 , △ABC的面积为;(2)、在所给的方格纸中,请你以原点O为位似中心,将△ABC缩小为原来的一半(仅用直尺);(3)、在(2)中,若P(a,b)为线段AC上的任一点,则缩小后点P的对应点P1的坐标为.(4)、按要求作图,不要求写作法,但要保留作图痕迹.
(1)、点B的坐标为 , △ABC的面积为;(2)、在所给的方格纸中,请你以原点O为位似中心,将△ABC缩小为原来的一半(仅用直尺);(3)、在(2)中,若P(a,b)为线段AC上的任一点,则缩小后点P的对应点P1的坐标为.(4)、按要求作图,不要求写作法,但要保留作图痕迹.我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.
请运用上述性质,只用直尺(不带刻度)作图.
①如图2,在平行四边形ABCD中,E为CD的中点,作BC的中点F.
②如图3,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH.