人教版数学九年级下册 第二十七章 相似 27.2.3 应用举例 同步练习
试卷更新日期：2021-01-02 类型：同步测试
一、单选题
-
1. 学校门口的栏杆如图所示，栏杆从水平位置 绕 点旋转到 位置，已知 ， ，垂足分别为 ， ， ， ， ，则栏杆 端应下降的垂直距离 为（ ）
A、
B、
C、
D、
2. 如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上。若测得BE=20m，EC=10m，CD=20m，则河的宽度AB等于（ ）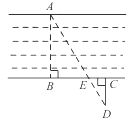
A、60m B、40m C、30m D、20m3. 如图，一电线杆AB的影子分别落在地上和墙上，某一时刻，小明竖起1m高的直杆，量得其影长为0.5m，此时，他又量得电线杆AB落在地上的影子BD长3m，落在墙上的影子CD的高为2m，小明用这些数据很快算出了电线杆AB的高，请你计算，电线杆AB的高为（ ）
A、5m B、6m C、7m D、8m4. 如图，小明同学用自制的直角三角形纸板 测量树的高度 ，他调整自己的位置，设法使斜边 保持水平，并且边 与点 在同一直线上.已知纸板的两条直角边 ， ，测得边 离地面的高度 ， ，则树高 是（ ）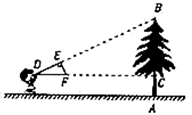
A、4米 B、4.5米 C、5米 D、5.5米5. 如图，为了估计某一条河的宽度，在河的对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S在一条直线上，且直线PS与河垂直，在过点S且与PS垂直的直线a上选择适当的点T，PT与过点Q且与PS垂直的直线b的交点为R，如果QS = 60m，ST =120m，QR=80m，则这条河的宽度PQ为（ ）
A、40m B、120m C、60m D、180m6.如图，路灯距地面8米，身高1.6米的小明从距离灯的底部（点O）20米的点A处，沿OA所在的直线行走14米到点B时，人影的长度( )
A、增大1.5米 B、减小1.5米 C、增大3.5米 D、减小3.5米二、填空题
-
7. 一棵高 米的小树影长为 米，同时临近它的一座楼房的影长是 米，这座楼房高米.8. 如图，某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC ， 已知栏杆AB的长为3.5米，OA的长为3米，点C到AB的距离为0.3米，支柱OE的高为0.6米，那么栏杆端点D离地面的距离为米
9. 一个斜坡长 米，高 米，把重物从坡底沿着斜坡推进 米后停下，此时物体的高度是米10. 如图，测量小玻璃管口径的量具ABC上，AB的长为10mm，AC被分为60等份，如果小管口DE正好对着量具上30份处（DE//AB），那么小管口径DE的长是mm．
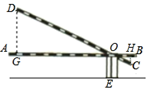
11. 如图，一电线杆 的影子分别落在了地上和墙上．同一时刻，小明竖起 米高的直杆 ，量得其影长 为 米，量得电线杆 落在地上的影子 长 米，落在墙上的影子 的高为 米，则电线杆 的高为米．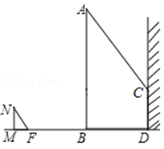
12. 《九章算术》是我国古代数学名著，书中有如下问题： “今有井径5尺，不知其深，立五尺木于井上，从木末 望水岸，入径四寸．问井深几何？”意思是：如图， 井径 尺，立木高 尺， 寸=0.4尺，则井深x为尺．
13.如图，李明打网球时，球恰好打过网，且落在离网4m的位置上，则网球的击球的高度h为 ．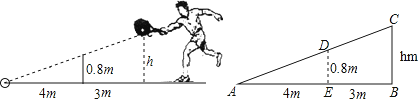
三、解答题
-
14. 如图，在阳光下，身高165cm的小军测得自己的影长为0.9m ， 同时还测得教学楼的影长为8.1m ， 求该教学楼的高度．
15. 某班在学习《利用相似三角形测高》时开展了“测量学校操场上旗杆高度"的活力，小明将镜子放在离旗杆32m的点C处(即AC=32m)，然后消自线AC后退，在点D处恰好看到旗杆顶端B在镜子中的像与镜子上的标记重合(如图)，根据物理学知织可知，法线l⊥AD于C，∠1=∠2。若小明的眼睛离地面的高度DE=1.5m，CD=3m，求旗杆的高度，(要有证明过程，再求值)
16. 据史料记载，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度．如图，如果木杆 长 ，它的影长 为 ，测得 为 ，求金字塔的高度 ．
17. 如图，一个油漆桶高75cm，桶内还有剩余的油漆，一根木棒长1m，小明将木棒从桶盖小口斜插入桶内，一端触到桶底边缘时，量得木棒露在桶外的部分长10cm．抽出小棒，又量得木棒上沾了油漆的部分长36cm，请计算桶内油漆的高度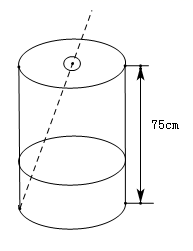
四、综合题
-
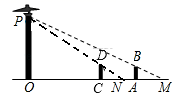
18. 学习了相似三角形的知识后，爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度，并作出了示意图：如图，路灯（点P）距地面若干米，身高1.6米的小明站在距路灯的底部（O点）20米的A点时，身影的长度AM为5米；
(1)、请帮助小明求出路灯距地面的高度；(2)、若另一名身高为1.5米小龙站在直线OA上的C点时，测得他与小明的距离AC为7米，求小龙的身影的长度．19. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度．(1)、如图1所示，淇淇将镜子放在地面上，然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E ， 测得脚掌中心位置B到镜面中心C的距离是50cm ， 镜面中心C距离旗杆底部D的距离为4m ， 已知淇淇同的身高是1.54m ， 眼睛位置A距离淇淇头顶的距离是4cm ， 求旗杆DE 的高度．
(2)、如图2所示，嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米，在同时刻测量旗杆的影长时，旗杆的影子一部分落在地面上（BC），另一部分落在斜坡上（CD），他测得落在地面上的影长为10米，落在斜坡上的影长为 米，∠DCE=45°，求旗杆AB的高度？