人教版数学九年级下册 第二十七章 相似 27.2.2 相似三角形的性质 同步练习
试卷更新日期:2021-01-02 类型:同步测试
一、单选题
-
1. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
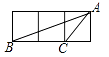 A、
A、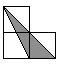 B、
B、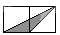 C、
C、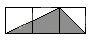 D、
D、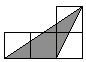 2. 如图,△ABC中,点D、E分别在AB、AC边上,则下列条件中,不一定能使△AED∽△ABC的是( )
2. 如图,△ABC中,点D、E分别在AB、AC边上,则下列条件中,不一定能使△AED∽△ABC的是( )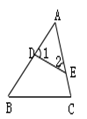 A、∠2=∠B B、∠1=∠C C、 D、3. 如图,已知△ABC∽△DAC,∠B=36º,∠D=117º,则∠BAD的度数为( )
A、∠2=∠B B、∠1=∠C C、 D、3. 如图,已知△ABC∽△DAC,∠B=36º,∠D=117º,则∠BAD的度数为( ) A、36º B、117º C、143º D、153º4. △ABC与△DEF的相似比为2:3,且△ABC的周长为40,则△DEF的周长是( )A、20 B、40 C、60 D、805. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BD交于点F,则S△DEF:S△ADF:S△ABF等于( )
A、36º B、117º C、143º D、153º4. △ABC与△DEF的相似比为2:3,且△ABC的周长为40,则△DEF的周长是( )A、20 B、40 C、60 D、805. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BD交于点F,则S△DEF:S△ADF:S△ABF等于( )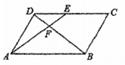 A、2:3:5 B、4:9:25 C、2:5:25 D、4:10:256. 将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )
A、2:3:5 B、4:9:25 C、2:5:25 D、4:10:256. 将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )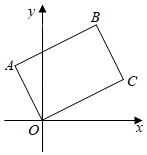 A、(4,2) B、(3, ) C、(3, ) D、(2, )
A、(4,2) B、(3, ) C、(3, ) D、(2, )二、填空题
-
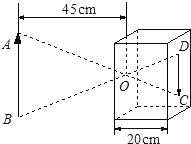
7. 当两个相似三角形的相似比为时,这两个相似三角形-定是-对全等三角形。8. 如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为cm.
 9. 如果两个相似三角形的面积比为4:9,那么这两个三角形的相似比为 .10. 如图,
9. 如果两个相似三角形的面积比为4:9,那么这两个三角形的相似比为 .10. 如图,
点P是矩形ABCD内一点,连接PA、PB、PC、PD , 已知AB=3,BC=4;则①PA+PB+PC+PD的最小值为;
②若△PAB∽△PDA , 则PA= .
11. 如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G , 则 .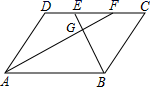 12. 在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=时,以A,D,E为顶点的三角形与△ABC相似.13. 如图,在 中, , ,点D为AC上一点,作 交BC于点E , 点C关于DE的对称点为点O , 以OA为半径作⊙O恰好经过点C , 并交直线DE于点M , N则MN的值为 .
12. 在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=时,以A,D,E为顶点的三角形与△ABC相似.13. 如图,在 中, , ,点D为AC上一点,作 交BC于点E , 点C关于DE的对称点为点O , 以OA为半径作⊙O恰好经过点C , 并交直线DE于点M , N则MN的值为 .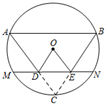
三、解答题
-
14. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E,若DE=4,BC=AE=6,求EC的长.
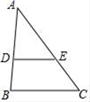 15. 在 中, 为BC边上的中线, 于点 的延长线交于点,求 的值
15. 在 中, 为BC边上的中线, 于点 的延长线交于点,求 的值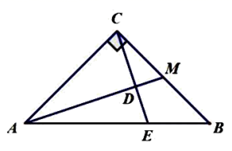 16. 如图,已知正方形ABCD中,BE平分 且交CD边于点E,延长BC至F使 ,联接DF,延长BE交DF于点G.求证: .
16. 如图,已知正方形ABCD中,BE平分 且交CD边于点E,延长BC至F使 ,联接DF,延长BE交DF于点G.求证: .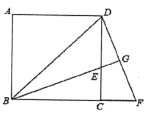 17. 已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.
17. 已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.
提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.
四、综合题
-
18. 如图,正方形ABCD中,M为BC上一点,点F是AM的中点,EF⊥AM,垂足为点F,交AD的延长线于点E,交DC于点N。
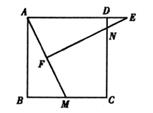 (1)、求证:△ABM∽△EFA;(2)、若AB=12,BM=5,求DE的长。
(1)、求证:△ABM∽△EFA;(2)、若AB=12,BM=5,求DE的长。