人教版数学九年级下册 第二十六章 反比例函数 单元测试卷
试卷更新日期:2021-01-02 类型:单元试卷
一、单选题
-
1. 已知反比例函数的图象经过点(1,3),则这个反比例函数的表达式为( )A、y= B、y= C、y= D、y=-2. 若双曲线y= 位于第二、四象限,则k的取值范围是( )A、k<1 B、k≥1 C、k>1 D、k≠13. 已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数 的图象在( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限.4. 反比例函数y= 的图象经过的象限是( )A、第一二象限 B、第一三象限 C、第二三象限 D、第二四象限5. 如图,函数 与 在同一平面直角坐标系中的图像大致( )A、
 B、
B、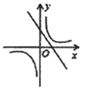 C、
C、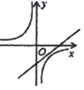 D、
D、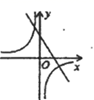 6. 根据表中的自变量x与函数y的对应值,可判断此函数解析式为( )
6. 根据表中的自变量x与函数y的对应值,可判断此函数解析式为( ) A、 B、 C、 D、7. 若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y38. 2019年10月,《长沙晚报》对外发布长沙高铁两站设计方案,该方案以三湘四水,杜鹃花开 ,塑造出杜鹃花开的美丽姿态,该高铁站建设初期需要运送大量的土石方,某运输公司承担了运送总量为 土石方的任务,该运输公司平均运送土石方的速度 (单位: 天)与完成运送任务所需的时间t(单位:天)之间的函数关系式是( )A、 B、 C、 D、9. 如图,在以 为原点的平面直角坐标系中,矩形 的两边 、 分别在 轴、 轴的正半轴上,反比例函数 的图象与 相交于点 ,与 相交于点 ,若 ,且 的面积是 ,则 的值为( ).
A、 B、 C、 D、7. 若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y38. 2019年10月,《长沙晚报》对外发布长沙高铁两站设计方案,该方案以三湘四水,杜鹃花开 ,塑造出杜鹃花开的美丽姿态,该高铁站建设初期需要运送大量的土石方,某运输公司承担了运送总量为 土石方的任务,该运输公司平均运送土石方的速度 (单位: 天)与完成运送任务所需的时间t(单位:天)之间的函数关系式是( )A、 B、 C、 D、9. 如图,在以 为原点的平面直角坐标系中,矩形 的两边 、 分别在 轴、 轴的正半轴上,反比例函数 的图象与 相交于点 ,与 相交于点 ,若 ,且 的面积是 ,则 的值为( ). A、 B、8 C、6 D、
A、 B、8 C、6 D、二、填空题
-
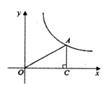
10. 已知y=(a-1)xa是反比例函数,则a的值是。11. 如图,在平面直角坐标系xOy中,点A在函数y= (x>0)的图象上,AC⊥x轴于点C,连接OA,则△OAC面积为 。
 12. 如图,一次函数 与反比例函数 的图像交于 、 两点,其横坐标分别为 和 ,则关于 的不等式 的解集是 .
12. 如图,一次函数 与反比例函数 的图像交于 、 两点,其横坐标分别为 和 ,则关于 的不等式 的解集是 . 13. 已知反比例函数 的图象上三个点的坐标分别是 , , ,则 , , 的大小关系是(用“< ”号连接).14. 某产品的进价为50元,该产品的日销量 (件)是日销价 (元)的反比例函数,且当售价为每件100元时,每日可售出40件,为获得日利润为1500元,售价应定为.15. 如图,等腰 的两个顶点 、 在反比例函数 ( )的图象上, .过点C作边 的垂线交反比例函数 ( )的图象于点D,动点P从点D出发,沿射线 方向运动 个单位长度,到达反比例函数 ( )图象上一点,则 .
13. 已知反比例函数 的图象上三个点的坐标分别是 , , ,则 , , 的大小关系是(用“< ”号连接).14. 某产品的进价为50元,该产品的日销量 (件)是日销价 (元)的反比例函数,且当售价为每件100元时,每日可售出40件,为获得日利润为1500元,售价应定为.15. 如图,等腰 的两个顶点 、 在反比例函数 ( )的图象上, .过点C作边 的垂线交反比例函数 ( )的图象于点D,动点P从点D出发,沿射线 方向运动 个单位长度,到达反比例函数 ( )图象上一点,则 .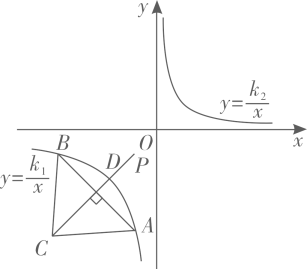
三、计算题
-
16.(1)、已知反比例函数y= ,当x=1时,y=3;试先求k值;(2)、解关于t的方程. .
四、解答题
-
17. 如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
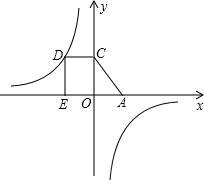 18. 如图,在平面系中,一次函数 的图像经过定点A,反比例函数 的图像经过点A,且与一次函数 的图像相交于点B( ,m).
18. 如图,在平面系中,一次函数 的图像经过定点A,反比例函数 的图像经过点A,且与一次函数 的图像相交于点B( ,m).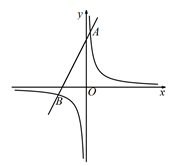 (1)、求m、a的值;(2)、设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式 的值.19. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)、求m、a的值;(2)、设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式 的值.19. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
五、综合题
-
20. 如图,Rt△ABO的顶点A是双曲线y= 与直线y=﹣x+(k+1)在第四象限的交点,AB⊥x轴于点B , 且S△ABO= .
 (1)、求这两个函数的表达式;(2)、求直线与双曲线的交点A和C的坐标及△AOC的面积.(3)、写出反比例函数y= 的值大于一次函数y=﹣x+(k+1)时的x的取值范围.21. 小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到下表数据:
(1)、求这两个函数的表达式;(2)、求直线与双曲线的交点A和C的坐标及△AOC的面积.(3)、写出反比例函数y= 的值大于一次函数y=﹣x+(k+1)时的x的取值范围.21. 小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到下表数据:x
0.5
1
1.5
2
3
4
6
12
y
12
6
4
3
2

1
0.5
结果发现一个数据被墨水涂黑了.
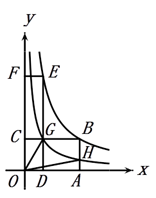
(1)、被墨水涂黑的数据为.(2)、y与x之间的函数关系式为(其中x>0),且y随x的增大而.(3)、如图是小明画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1 , 矩形ODEF的面积记为S2 , 请判断S1和S2的大小关系,并说明理由.(4)、在(3)的条件下,DE交BC于点G,反比例函数y= 的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为.
-