《初中数学北师大版九年级下学期 第一章 单元测试卷》
试卷更新日期:2021-01-02 类型:单元试卷
一、单选题
-
1. 在Rt△ABC中,∠C=90°,∠B=40°,AB=10,则直角边BC的长是( )A、10sin40° B、 10cos40° C、10tan40° D、2. 若∠A是锐角,且sinA= ,则( )A、0º<∠A<30º B、30º<∠A<45º C、45º<∠A<60º D、60º<∠A<90º3. 如果a是锐角,且cosa= ,那么sina的值是( )A、 B、 C、 D、4. 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
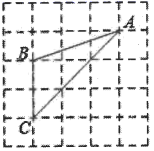 A、 B、 C、2 D、5. 如图, 在 中, , , , 则 的值是( )
A、 B、 C、2 D、5. 如图, 在 中, , , , 则 的值是( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,直线 过点 ,则 的值是( ).
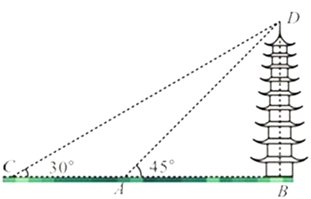
A、 B、 C、 D、6. 如图,在平面直角坐标系中,直线 过点 ,则 的值是( ).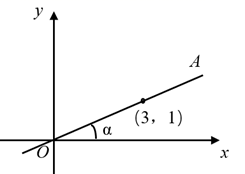 A、 B、 C、 D、37. 在Rt△ABC中,∠C=90°, 、 、 所对的边分别为a、b、c , 如果a=3b , 那么∠A的余切值为( )A、 B、3 C、 D、8. 在Rt 中,∠C=90°,如果AC=2, ,那么AB的长是( )A、 B、 C、 D、9. 某兴趣小组想测量一座大楼 AB的高度.如图,大楼前有一段斜坡BC ,已知 BC的长为 12 米它的坡度 .在离 C点 40 米的 D处,用测量仪测得大楼顶端 A的仰角为 37度,测角仪DE的高度为 1.5米,求大楼AB 的高度约为( )米( )
A、 B、 C、 D、37. 在Rt△ABC中,∠C=90°, 、 、 所对的边分别为a、b、c , 如果a=3b , 那么∠A的余切值为( )A、 B、3 C、 D、8. 在Rt 中,∠C=90°,如果AC=2, ,那么AB的长是( )A、 B、 C、 D、9. 某兴趣小组想测量一座大楼 AB的高度.如图,大楼前有一段斜坡BC ,已知 BC的长为 12 米它的坡度 .在离 C点 40 米的 D处,用测量仪测得大楼顶端 A的仰角为 37度,测角仪DE的高度为 1.5米,求大楼AB 的高度约为( )米( )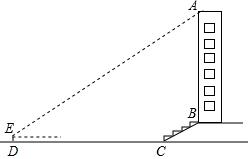 A、39.3 B、37.8 C、33.3 D、25.710. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A、39.3 B、37.8 C、33.3 D、25.710. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )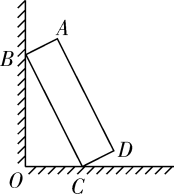 A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx
A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx二、填空题
-
11. 已知∠A是锐角,且tanA= ,则sin = .12. 如图,当小明沿坡度i=1: 的坡面由A到B行走了6米时,他实际上升的高度BC=米.
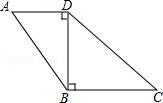
 13. 如果α是锐角,且sinα=cos20°,那么α=度.14. 若sinα= cos60°,则锐角α=.15. 某人从地面沿着坡度为 的山坡走了 米,这时他离地面的高度是米.16. 如图,在四边形ABCD中,AB= ,AD=7,BC=8,tan ∠B= ,∠C=∠D,则线段CD的长为 .
13. 如果α是锐角,且sinα=cos20°,那么α=度.14. 若sinα= cos60°,则锐角α=.15. 某人从地面沿着坡度为 的山坡走了 米,这时他离地面的高度是米.16. 如图,在四边形ABCD中,AB= ,AD=7,BC=8,tan ∠B= ,∠C=∠D,则线段CD的长为 .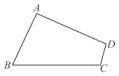
三、计算题
-
17. 计算:18. 计算: .
四、解答题
-
19. 我们把底角为51°的等腰三角形称为最稳定三角形. 如图,已知△ABC是最稳定三角形, AB=AC,BC=232.8m.求BC边上的高AD的长.
(sin51°≈0.8,cos51°≈0.6,tan51°≈1.2,精确到1m)
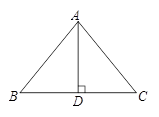 20. 如图,在△ABC中, , , ,求AB的长.
20. 如图,在△ABC中, , , ,求AB的长.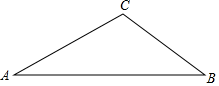 21. 周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
21. 周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)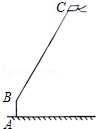 ]
]