2016年浙江省台州市中考数学试卷
试卷更新日期:2016-07-01 类型:中考真卷
一、选择题
-
1. 下列各数中,比﹣2小的数是( )A、﹣3 B、﹣1 C、0 D、22.
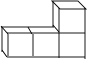
如图所示几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 我市今年一季度国内生产总值为77643000000元,这个数用科学记数法表示为( )A、0.77643×1011 B、7.7643×1011 C、7.7643×1010 D、77643×1064. 下列计算正确的是( )A、x2+x2=x4 B、2x3﹣x3=x3 C、x2•x3=x6 D、(x2)3=x55. 质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )A、点数都是偶数 B、点数的和为奇数 C、点数的和小于13 D、点数的和小于26. 化简 的结果是( )A、﹣1 B、1 C、 D、7.
3. 我市今年一季度国内生产总值为77643000000元,这个数用科学记数法表示为( )A、0.77643×1011 B、7.7643×1011 C、7.7643×1010 D、77643×1064. 下列计算正确的是( )A、x2+x2=x4 B、2x3﹣x3=x3 C、x2•x3=x6 D、(x2)3=x55. 质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )A、点数都是偶数 B、点数的和为奇数 C、点数的和小于13 D、点数的和小于26. 化简 的结果是( )A、﹣1 B、1 C、 D、7.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
 A、 B、 C、 D、8. 有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )A、x(x﹣1)=45 B、x(x+1)=45 C、x(x﹣1)=45 D、x(x+1)=459. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )A、1次 B、2次 C、3次 D、4次10.
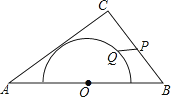
A、 B、 C、 D、8. 有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )A、x(x﹣1)=45 B、x(x+1)=45 C、x(x﹣1)=45 D、x(x+1)=459. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )A、1次 B、2次 C、3次 D、4次10.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
 A、6 B、2 +1 C、9 D、
A、6 B、2 +1 C、9 D、二、填空题
-
11. 因式分解:x2﹣6x+9= .
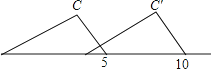
12.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC′= .
 13.
13.如图,△ABC的外接圆O的半径为2,∠C=40°,则 的长是 .
 14. 不透明袋子中有1个红球、2个黄球,这些球除颜色外无其他差别,从袋子中随机摸出1个球后放回,再随机摸出1个球,两次摸出的球都是黄球的概率是 .
14. 不透明袋子中有1个红球、2个黄球,这些球除颜色外无其他差别,从袋子中随机摸出1个球后放回,再随机摸出1个球,两次摸出的球都是黄球的概率是 .
15.如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是 .
 16. 竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
16. 竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
三、解答题
-
17. 计算: ﹣|﹣ |+2﹣1 .18. 解方程: ﹣ =2.19.
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
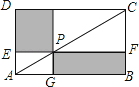 (1)、求证:△PHC≌△CFP;(2)、证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.20.
(1)、求证:△PHC≌△CFP;(2)、证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.20.保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
 21.
21.请用学过的方法研究一类新函数y= (k为常数,k≠0)的图象和性质.
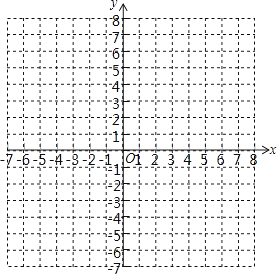 (1)、在给出的平面直角坐标系中画出函数y= 的图象;(2)、对于函数y= ,当自变量x的值增大时,函数值y怎样变化?22.
(1)、在给出的平面直角坐标系中画出函数y= 的图象;(2)、对于函数y= ,当自变量x的值增大时,函数值y怎样变化?22.为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
分组
频数
4.0≤x<4.2
2
4.2≤x<4.4
3
4.4≤x<4.6
5
4.6≤x<4.8
8
4.8≤x<5.0
17
5.0≤x<5.2
5
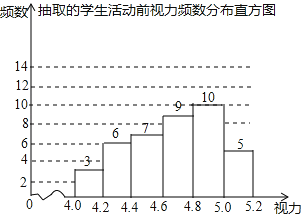 (1)、求所抽取的学生人数;(2)、若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;(3)、请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.23.
(1)、求所抽取的学生人数;(2)、若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;(3)、请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.23.定义:有三个内角相等的四边形叫三等角四边形.
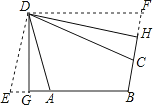 (1)、三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;(2)、如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.(3)、三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.24.
(1)、三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;(2)、如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.(3)、三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.24.【操作发现】在计算器上输入一个正数,不断地按“ ”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后再x轴上确定对应的数x2 , …,以此类推.
【解决问题】研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
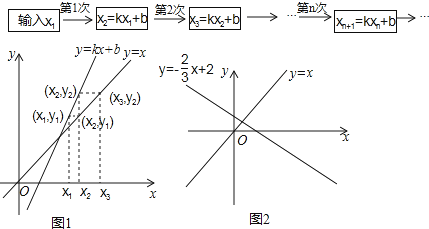 (1)、若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;(2)、若k>1,又得到什么结论?请说明理由;(3)、①若k=﹣ ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;
(1)、若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;(2)、若k>1,又得到什么结论?请说明理由;(3)、①若k=﹣ ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)