2016年浙江省丽水市中考数学试卷

试卷更新日期：2016-07-01 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列四个数中，与﹣2的和为0的数是（　　）

A、﹣2 B、2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 计算3²×3^﹣¹的结果是（　　）

A、3 B、﹣3 C、2 D、﹣2

查看试题解析
3. 下列图形中，属于立体图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. $\frac{1}{a}$ + $\frac{1}{b}$ 的运算结果正确的是（　　）

A、 $\frac{1}{a + b}$ B、 $\frac{2}{a + b}$ C、 $\frac{a + b}{a b}$ D、a+b

查看试题解析
5. 某校对全体学生开展心理健康知识测试，七、八、九三个年级共有800名学生，各年级的合格人数如表所示，则下列说法正确的是（　　）
年级
七年级
八年级
九年级
合格人数
270
262
254

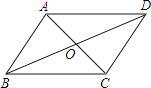
A、七年级的合格率最高 B、八年级的学生人数为262名 C、八年级的合格率高于全校的合格率 D、九年级的合格人数最少

查看试题解析
6. 下列一元二次方程没有实数根的是（　　）

A、x²+2x+1=0 B、x²+x+2=0 C、x²﹣1=0 D、x²﹣2x﹣1=0

查看试题解析
7.
如图，▱ABCD的对角线AC，BD交于点O，已知AD=8，BD=12，AC=6，则△OBC的周长为（　　）

A、13 B、17 C、20 D、26

查看试题解析
8. 在直角坐标系中，点M，N在同一个正比例函数图象上的是（　　）

A、M（2，﹣3），N（﹣4，6） B、M（﹣2，3），N（4，6） C、M（﹣2，﹣3），N（4，﹣6） D、M（2，3），N（﹣4，6）

查看试题解析
9. 用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（　　）

A、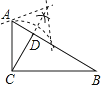 B、 C、 D、

查看试题解析
10.
如图，已知⊙O是等腰Rt△ABC的外接圆，点D是 $\overset{\land}{A C}$ 上一点，BD交AC于点E，若BC=4，AD= $\frac{4}{5}$ ，则AE的长是（　　）

A、3 B、2 C、1 D、1.2

查看试题解析

二、填空题

11. 分解因式：am﹣3a= ．

查看试题解析
12.
如图，在△ABC中，∠A=63°，直线MN∥BC，且分别与AB，AC相交于点D，E，若∠AEN=133°，则∠B的度数为．

查看试题解析
13. 箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是．

查看试题解析
14. 已知x²+2x﹣1=0，则3x²+6x﹣2= ．

查看试题解析
15. 如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为点E，F，延长BD至G，使得DG=BD，连结EG，FG，若AE=DE，则 $\frac{E G}{A B}$ = ．

查看试题解析
16.
如图，一次函数y=﹣x+b与反比例函数y= $\frac{4}{x}$ （x＞0）的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连结OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m．

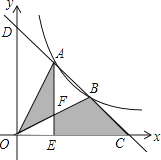(1)、b=（用含m的代数式表示）；

(2)、若S_△_OAF+S_四边形_EFBC=4，则m的值是．

查看试题解析

三、解答题

17. 计算：（﹣3）⁰﹣|﹣ $\sqrt{2}$ |+ $\sqrt{8}$ ．

查看试题解析
18. 解不等式：3x﹣5＜2（2+3x）

查看试题解析
19.
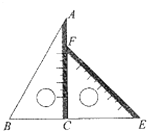
数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含45°的三角板的斜边与含30°的三角板的长直角边相等，于是，小陆同学提出一个问题：如图，将一副三角板直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC=2，求AF的长．
请你运用所学的数学知识解决这个问题.

查看试题解析
20.
为了帮助九年级学生做好体育考试项目的选考工作，某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩，并绘制成如图两个统计图，请结合统计图信息解决问题．

(1)、“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍，求“跳绳”项目的女生人数；

(2)、若一个考试项目的男、女生总平均成绩不小于9分为“优秀”，试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目，并说明理由；

(3)、请结合统计图信息和实际情况，给该校九年级学生体育考试项目的选择提出合理化建议．

查看试题解析
21.
2016年3月27日“丽水半程马拉松竞赛”在莲都举行，某运动员从起点万地广场西门出发，途经紫金大桥，沿比赛路线跑回中点万地广场西门．设该运动员离开起点的路程S（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，根据图象提供的信息，解答下列问题：

(1)、求图中a的值；

(2)、组委会在距离起点2.1千米处设立一个拍摄点C，该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟．
①求AB所在直线的函数解析式；
②该运动员跑完赛程用时多少分钟？

查看试题解析
22.
如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD，BC的延长线相交于点E．

(1)、求证：AD是半圆O的切线；

(2)、连结CD，求证：∠A=2∠CDE；

(3)、若∠CDE=27°，OB=2，求 $\overset{\land}{B D}$ 的长．

查看试题解析
23.
如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y= $\frac{1}{10}$ x²﹣ $\frac{4}{5}$ x+3的绳子．

(1)、求绳子最低点离地面的距离；

(2)、因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F₁的最低点距MN为1米，离地面1.8米，求MN的长；

(3)、将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F₂对应函数的二次项系数始终为 $\frac{1}{4}$ ，设MN离AB的距离为m，抛物线F₂的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．

查看试题解析
24.
如图，矩形ABCD中，点E为BC上一点，F为DE的中点，且∠BFC=90°．

(1)、当E为BC中点时，求证：△BCF≌△DEC；

(2)、当BE=2EC时，求 $\frac{C D}{B C}$ 的值；

(3)、设CE=1，BE=n，作点C关于DE的对称点C′，连结FC′，AF，若点C′到AF的距离是 $\frac{2 \sqrt{10}}{5}$ ，求n的值．

查看试题解析

年级	七年级	八年级	九年级
合格人数	270	262	254