浙江省宁波市慈溪市2020-2021学年七年级上学期数学12月月考试卷

试卷更新日期：2020-12-31 类型：月考试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．）

1. -（-3）的倒数是（）

A、 $- \frac{1}{3}$ B、-3 C、 $\frac{1}{3}$ D、3

查看试题解析
2. 习近平总书记提出了五年“精准扶贫”的战略构想，意味着每年要减贫11700000人，数据11700000用科学记数法表示为（）

A、1.17×10⁷ B、11.7×10⁶ C、1.17×10⁵ D、117×10⁵

查看试题解析
3. 若∠1=40°，则∠1的补角为（）

A、50° B、60° C、140° D、160°

查看试题解析
4. 如图， $\sqrt{5}$ 表示在数轴上的位置正确的是（）

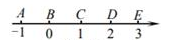A、点A、B之间 B、点B、C之间 C、点C、D之间 D、点D、E之间

查看试题解析
5. 下列方程中，是一元一次方程的是（）

A、2y-3x=5 B、y-3=5y+1 C、 $\frac{1}{2}$ x-3= $\frac{x}{2}$ D、y²-2y+3=0

查看试题解析
6. 将 $- \frac{1}{2} (y - 2 x)$ 去括号，得（）

A、 $- \frac{1}{2}$ y+2x B、 $- \frac{1}{2} y - 2 x$ C、 $- \frac{1}{2} y + x$ D、 $- \frac{1}{2} y - x$

查看试题解析
7. 如图，下列说法正确的是（）

A、直线AB与直线BC是同一条直线 B、线段AB与线段BA是不同的两条线段 C、射线AB与射线AC是两条不同的射线 D、射线BC与射线BA是同一条射线

查看试题解析
8. 下列判断正确的是（　　）

A、3a²bc与bca²不是同类项 B、 $\frac{2 m^{2} n}{5}$ 的系数是2 C、单项式﹣x³yz的次数是5 D、3x²﹣y+5xy⁵是二次三项式

查看试题解析
9. 如图，小李同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（）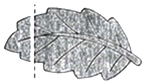

A、垂线段最短 B、经过一点有无数条直线 C、两点之间线段最短 D、经过两点有且仅有一条直线

查看试题解析
10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm，宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（）

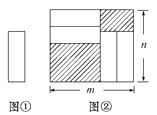A、4mcm B、4ncm C、2(m+n)cm D、4(m-n)cm

查看试题解析

二、填空题（本题有10小题，每小题3分，共30分）

11. 计算：-8×4= ．

查看试题解析
12. 合并同类项：4a²-a²= ．

查看试题解析
13. 如图，∠ABC=90°，∠CBD=45°，BP平分∠ABD，则∠ABP的度数是°.

查看试题解析
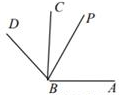14. 一件商品按成本价提高30%后标价，又以8折销售，售价为208元这种商品的成本价是元。

查看试题解析
15. 将0.09493用四舍五入法取近似值精确到百分位，其结果是.

查看试题解析
16. 已知一个多项式与3x²+9x+2的和等于3x²+4x﹣3，则此多项式是.

查看试题解析
17. 有一个数值转换器，原理如图．当输入x的值为25时，输出y的值是．

查看试题解析
18. 某校组织七年级学生参加研学活动，如果单独租用45座车若干辆，则刚好坐满；如果单独租用60座客车，则可少租2辆，并且剩余15座．该校参加研学活动的有人．

查看试题解析
19. 把53°30′用度表示为.

查看试题解析
20. 当x=l时，代数式ax³-3bx+5的值是2019，则当x=-l时，这个代数式的值是.

查看试题解析

三、解答题(本题有8小题，共60分)

21. 计算

(1)、 $- 1^{2} + \sqrt{9} - | - 5 |$

(2)、 $24 \times (\frac{5}{6} - \frac{1}{4})$

查看试题解析
22. 解下列方程

(1)、3x-4=x

(2)、 $\frac{x - 1}{2} = 1 - \frac{x - 1}{4}$

查看试题解析
23. 先化简，再求值：
$2 (\frac{1}{2} b - 1) - 3 (- \frac{1}{3} a^{2} + b - 2)$ ，其中a=-1，b=1.

查看试题解析
24. 如图所示，已知点A，B，C，D，请按要求画出图形

（1）画直线AB和射线CB；
（2）连结AC，并在直线AB上用直尺和圆规作线段AE，使AE=2AC(要求保留作图痕迹)；
（3）在直线AB上确定一点P，使PC+PD的和最短，并写出画图的依据CBAD。

查看试题解析
25. 某文艺团体演出的全价票为每张18元，学生享受半价，某场演出共售出966张票，收入15480元，问：这场演出共售出学生票多少张？

查看试题解析
26. 如图，已知直线AD与BE相交于点O，∠DOE与∠COE互余，∠COE=62°，求∠AOB的度数.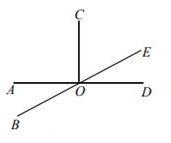

查看试题解析
27. 某体育用品商店对甲、乙两种品牌的足球开展促销活动，已知甲、乙两种品牌的足球的标价分别是160元/个，60元/个，现有如下两种优惠方案；方案一：未购买会员卡时，甲品牌足球享受八五折优惠，乙品牌足球买5个（含5个）以上时所有足球享受八五折，5个以下必须按标价购买方案二：办理一张会员卡100元，会员卡只限本人使用，全部商品享受七五折优惠

(1)、若购买甲品牌足球3个，乙品牌足球4个，哪一种方案更优惠？优惠了多少元？

(2)、如果购买甲品牌足球若干个，乙品牌足球6个，方案一与方案二所付钱数一样多，求购买甲品牌的足球的个数

查看试题解析
28. 如图，在数轴上点A表示的数a、点B表示数b，a、b满足|a﹣40|+（b+8）²＝0．点O是数轴原点．

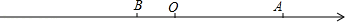(1)、点A表示的数为，点B表示的数为，线段AB的长为．

(2)、若点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，请在数轴上找一点C，使AC＝2BC，则点C在数轴上表示的数为．

(3)、现有动点P、Q都从B点出发，点P以每秒1个单位长度的速度向终点A移动；当点P移动到O点时，点Q才从B点出发，并以每秒3个单位长度的速度向右移动，且当点P到达A点时，点Q就停止移动，设点P移动的时间为t秒，问：当t为多少时，P、Q两点相距4个单位长度？

查看试题解析