初中数学浙教版2020-2021年八年级上学期数学期末模拟试卷
试卷更新日期:2020-12-31 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点 M到x轴的距离为 3,到y轴的距离为2,且在第四象限内,则点M的坐标为( )A、(-2,3) B、(2,-3) C、(3,2) D、不能确定3. 在等腰三角形ABC中,它的两边长分别为8cm和4cm,则它的周长为( )A、10cm B、12 cm C、20 cm或16 cm D、20 cm4. 下列图形中具有稳定性的是( )A、
2. 已知点 M到x轴的距离为 3,到y轴的距离为2,且在第四象限内,则点M的坐标为( )A、(-2,3) B、(2,-3) C、(3,2) D、不能确定3. 在等腰三角形ABC中,它的两边长分别为8cm和4cm,则它的周长为( )A、10cm B、12 cm C、20 cm或16 cm D、20 cm4. 下列图形中具有稳定性的是( )A、 B、
B、 C、
C、 D、
D、 5. 有下列语句:①两点之间,线段最短;②画两条平行的直线:③过直线外一点作已知直线的垂线:④如果两个角的和是90°,那么这两个角互余。其中是命题的有( )A、①② B、③④ C、②③ D、①④6. 小明用20元零花钱购买水果慰问老人,已知水果单价是每千克4元,设购买水果x千克用去的钱为y元,用图象表示y与x的函数关系,其中正确的是( )A、
5. 有下列语句:①两点之间,线段最短;②画两条平行的直线:③过直线外一点作已知直线的垂线:④如果两个角的和是90°,那么这两个角互余。其中是命题的有( )A、①② B、③④ C、②③ D、①④6. 小明用20元零花钱购买水果慰问老人,已知水果单价是每千克4元,设购买水果x千克用去的钱为y元,用图象表示y与x的函数关系,其中正确的是( )A、 B、
B、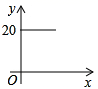 C、
C、 D、
D、 7. 如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( ).
7. 如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( ).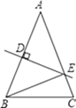 A、8 B、9 C、10 D、118. 已知等腰三角形的顶角为40°,则这个等腰三角形的底角为( )A、140° B、80° C、70° D、50°9. 如图,∠A+∠B +∠C +∠D +∠E等于( )
A、8 B、9 C、10 D、118. 已知等腰三角形的顶角为40°,则这个等腰三角形的底角为( )A、140° B、80° C、70° D、50°9. 如图,∠A+∠B +∠C +∠D +∠E等于( ) A、180° B、360° C、540° D、720°10. 如图,在△AOB和△COD中,OA=OB , OC=OD , OA<OC , ∠AOB=∠COD=36°.连接AC , BD交于点M , 连接OM . 下列结论:①∠AMB=36°;②AC=BD;③OM平分∠AOD;④MO平分∠AMD . 其中正确的有( )
A、180° B、360° C、540° D、720°10. 如图,在△AOB和△COD中,OA=OB , OC=OD , OA<OC , ∠AOB=∠COD=36°.连接AC , BD交于点M , 连接OM . 下列结论:①∠AMB=36°;②AC=BD;③OM平分∠AOD;④MO平分∠AMD . 其中正确的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 点 关于x轴对称的点的坐标为 .12. 一次函数 的图像不经过第象限.13. 中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-3,-2),“炮”位于点(-2,0),则“兵”位于的点的坐标为
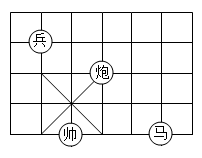 14. 如果三角形的两边长分别是3 cm和6 cm,第三边长是奇数,那么这个三角形的第三边长为cm.15. 如图,四边形OABC为正方形,边长为10,点A , C分别在x轴、y轴的正半轴上,点D在OA上,且D点的坐标为(4,0),P是OB上的一个动点,则PD+PA的最小值是 .
14. 如果三角形的两边长分别是3 cm和6 cm,第三边长是奇数,那么这个三角形的第三边长为cm.15. 如图,四边形OABC为正方形,边长为10,点A , C分别在x轴、y轴的正半轴上,点D在OA上,且D点的坐标为(4,0),P是OB上的一个动点,则PD+PA的最小值是 .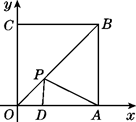 16. 如图是学校艺术馆中的柱子,高4.5m . 为迎接艺术节的到来,工作人员用一条花带从柱底向柱顶均匀地缠绕3圈,一直缠到起点的正上方为止.若柱子的底面周长是2m , 则这条花带至少需要m .
16. 如图是学校艺术馆中的柱子,高4.5m . 为迎接艺术节的到来,工作人员用一条花带从柱底向柱顶均匀地缠绕3圈,一直缠到起点的正上方为止.若柱子的底面周长是2m , 则这条花带至少需要m .
三、综合题
-
17. 解下列不等式:(1)、(2)、解不等式组18. 如图,在 中,AB=AC , AD是中线,CE∥AD交BA的延长线于点E . 请判断 的形状,并说明理由.
结论: 是三角形.

解:∵AB=AC , BD=CD (已知),
∴∠BAD=∠CAD( ▲ ).
∵CE∥AD (已知),
∴∠BAD= ▲ , ∠CAD= ▲ .
∴∠ACE =∠E .
∴AC=AE( ▲ ).
即△AEC是 ▲ 三角形.
19. 如图,在 中, , 分别是 的高和角平分线,若 , ,求 的度数.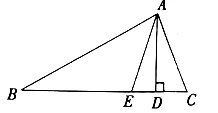 20. 某公司要印制新产品宣传材料.甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙厂提出:300张以内(含300张)每份材料收2.5元印制费,超出部分每张减少0.1元,不收制版费.(1)、分别写出两厂的收费y(元)与印制数量x(份)之间的关系式.(2)、印制800份宣传材料时,选择哪家印刷厂比较合算?21. 已知:△A1B1C1三个顶点的坐标分别为A1(﹣3,4),B1(﹣1,3),C1(1,6),把△A1B1C1先向右平移3个单位长度,再向下平移3个单位长度后得到△ABC , 且点A1的对应点为A , 点B1的对应点为B , 点C1的对应点为C .
20. 某公司要印制新产品宣传材料.甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙厂提出:300张以内(含300张)每份材料收2.5元印制费,超出部分每张减少0.1元,不收制版费.(1)、分别写出两厂的收费y(元)与印制数量x(份)之间的关系式.(2)、印制800份宣传材料时,选择哪家印刷厂比较合算?21. 已知:△A1B1C1三个顶点的坐标分别为A1(﹣3,4),B1(﹣1,3),C1(1,6),把△A1B1C1先向右平移3个单位长度,再向下平移3个单位长度后得到△ABC , 且点A1的对应点为A , 点B1的对应点为B , 点C1的对应点为C . (1)、在坐标系中画出△ABC;(2)、求△ABC的面积;(3)、设点P在y轴上,且△APB与△ABC的面积相等,求点P的坐标.22. 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B , 且与正比例函数y=kx的图象交点为C(3,4).
(1)、在坐标系中画出△ABC;(2)、求△ABC的面积;(3)、设点P在y轴上,且△APB与△ABC的面积相等,求点P的坐标.22. 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B , 且与正比例函数y=kx的图象交点为C(3,4). (1)、求k值与一次函数y=k1x+b的解析式;(2)、在x轴上有一动点P , 求当PB+PC最小时P点坐标.(3)、若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(1)、求k值与一次函数y=k1x+b的解析式;(2)、在x轴上有一动点P , 求当PB+PC最小时P点坐标.(3)、若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;

