甘肃省兰州市教学管理第五片区2019-2020学年七年级上学期数学期末考试卷
试卷更新日期:2020-12-31 类型:期末考试
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 正方体的截面中,边数最多的多边形是( )A、四边形 B、五边形 C、六边形 D、七边形3. 由陈凯歌、张一白、管虎等七位导演执导的电影《我和我的祖国》于2019年9月30日在全国上映,电影票房便超过299400000元,数299400000用科学记数法表为( )A、0.2994×109 B、2.994×108 C、29.94×107 D、2994×1064. 下列运算正确的是( )A、2a2﹣a2=1 B、5a2b﹣3ba2=2a2b C、5a+a=6a2 D、3a+3b=8ab5. 正方体的展开图可能是( )A、
 B、
B、 C、
C、 D、
D、 6. 下列事件中,最适合采用普查的是( )A、对我校七年级一班学生出生日期的调查 B、对全国中学生节水意识的调查 C、对山东省初中学生每天阅读时间的调查 D、对某批次灯泡使用寿命的调查7. 若﹣3xy2m与5x2n﹣3y6是同类项,则m、n的值分别是( )A、m=2,n=2 B、m=2,n=1 C、m=3,n=2 D、m=2,n=38. 已知扇形的半径为6,圆心角为60°,则这个扇形的面积为( )A、9π B、6π C、3π D、π9. 如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°,若∠AOC=40°,则∠DOE为( )
6. 下列事件中,最适合采用普查的是( )A、对我校七年级一班学生出生日期的调查 B、对全国中学生节水意识的调查 C、对山东省初中学生每天阅读时间的调查 D、对某批次灯泡使用寿命的调查7. 若﹣3xy2m与5x2n﹣3y6是同类项,则m、n的值分别是( )A、m=2,n=2 B、m=2,n=1 C、m=3,n=2 D、m=2,n=38. 已知扇形的半径为6,圆心角为60°,则这个扇形的面积为( )A、9π B、6π C、3π D、π9. 如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°,若∠AOC=40°,则∠DOE为( ) A、15° B、20° C、30° D、45°10. 下列说法:
A、15° B、20° C、30° D、45°10. 下列说法:①过两点有且只有一条直线;
②连接两点的线段叫两点的距离;
③两点之间线段最短;
④如果AB=BC,则点B是AC的中点.
其中正确的有( )
A、1个 B、2个 C、3个 D、4个11. 有一玻璃密封器皿如图①,测得其底面直径为20厘米,高20厘米,先内装蓝色溶液若干.若如图②放置时,测得液面高10厘米;若如图③放置室,测得液面高16厘米;则该玻璃密封器皿总容量为( )立方厘米.(结果保留 )
图① 图② 图③
A、1250 B、1300 C、1350 D、140012. 如图,第(1)个多边形由正三角形“扩展而来边数记为a3=12,第(2)个多边形由正方形“扩展”而来,边数记为a4=20,第(3)个多边形由五边形“扩展”而来,边数记为a5=30…依此类推,由正n边形“扩展而来的多边形的边数记为an(n≥3),则 结果是( )

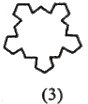
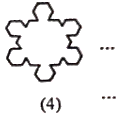 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知关于x的方程3x+a=4的解是x=1,则a的值是.14. 已知|a﹣3|+(b+1)2=0,则3a+b2011=.15. 下列说法中,正确的是.(填序号)
①一个有理数的绝对值一定是正数;
②正数和负数统称为有理数;
③若x+2是一个负数,则x一定是负数;
④六边形的对角线一共有9条
16. 如图,点C在线段AB上,AC:BC=3:2,点M是AB的中点,点N是BC的中点,若AB=10cm,则线段MN的长.
三、解答题
-
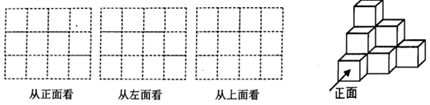
17. 计算:(1)、计算: .(2)、计算:﹣12020﹣1÷6×[3﹣(﹣3)2]﹣|﹣2|;18. 解方程:(1)、4x﹣1=x+2;(2)、 .19. 先化简再求值:3x2y﹣[2x2y﹣3(2xy﹣x2y)﹣xy],其中x= ,y=2.20. 如图,由几个相同的小正方体搭成一个几何体,请画出这个几何体的三种视图.(在所提供的方格内涂上相应的阴影即可)
 21. 某班学生的平均身高为152cm,如表列出了该班5名学生身高的部分情况(单位为cm):
21. 某班学生的平均身高为152cm,如表列出了该班5名学生身高的部分情况(单位为cm):姓名
小刚
小华
小强
小瑜
小奇
身高与平均值的差值
+10
﹣8
+4
﹣7
+15
(1)、小强和小瑜的身高分别是多少?(2)、这5名学生中最高与最矮的身高相差多少?22. 某地下停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场的小型汽车数量是中型汽车的3倍,这些车共缴纳停车费270元,则小型汽车有多少辆?23. 已知:如图, ,点 是线段 的中点,点 把线段 分成 的两部分,求线段 的长.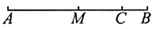
请补充下列解答过程:
解:因为 是线段 的中点,且 ,
所以 _▲_ _▲__ .
因为 ,
所以 _▲_ _▲_ .
所以 _▲_ __▲__ __▲_ _▲__ .
24. 某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如图不完整的条形统计图和扇形统计图(部分信息未给出) (1)、求本次调查学生的人数.(2)、求喜爱足球、跑步的人数,并补全条形统计图;(3)、求喜爱篮球、跑步的人数占调查人数的百分比.25. 一件商品按进价提高40%后标价,然后打八折卖出,结果仍能获利18元,问这件商品的进价是多少元?26. 有理数 、 、 在数轴上的位置如图:
(1)、求本次调查学生的人数.(2)、求喜爱足球、跑步的人数,并补全条形统计图;(3)、求喜爱篮球、跑步的人数占调查人数的百分比.25. 一件商品按进价提高40%后标价,然后打八折卖出,结果仍能获利18元,问这件商品的进价是多少元?26. 有理数 、 、 在数轴上的位置如图: (1)、判断正负,用“>”或“<”填空: -c0, + 0,c- 0.(2)、化简:|b-c|+| +b|-|c-a|27. 如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=18°,求∠AOC的度数.
(1)、判断正负,用“>”或“<”填空: -c0, + 0,c- 0.(2)、化简:|b-c|+| +b|-|c-a|27. 如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=18°,求∠AOC的度数. 28. 如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).(1)、观察一个等比列数1, ,…,它的公比q=;如果an(n为正整数)表示这个等比数列的第n项,那么a18= , an=;(2)、如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
28. 如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).(1)、观察一个等比列数1, ,…,它的公比q=;如果an(n为正整数)表示这个等比数列的第n项,那么a18= , an=;(2)、如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以
请根据以上的解答过程,求3+32+33+…+323的值;
(3)、用由特殊到一般的方法探索:若数列a1 , a2 , a3 , …,an , 从第二项开始每一项与前一项之比的常数为q,请用含a1 , q,n的代数式表示an;如果这个常数q≠1,请用含a1 , q,n的代数式表示a1+a2+a3+…+an.