甘肃省白银市靖远县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-12-31 类型:期末考试
一、单选题
-
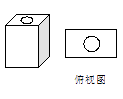
1. 某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是 ( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,已知直线a∥b∥c , 直线m、n与a、b、c分别交于点A、C、E、B、D、F , 若AC=8,CE=12,BD=6,则BF的值是( )
2. 如图,已知直线a∥b∥c , 直线m、n与a、b、c分别交于点A、C、E、B、D、F , 若AC=8,CE=12,BD=6,则BF的值是( )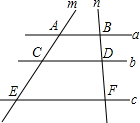 A、14 B、15 C、16 D、173. 用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )A、(x+3)2=1 B、(x﹣3)2=1 C、(x+3)2=19 D、(x﹣3)2=194. 当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P= (S≠0),这个函数的图象大致是( )A、
A、14 B、15 C、16 D、173. 用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )A、(x+3)2=1 B、(x﹣3)2=1 C、(x+3)2=19 D、(x﹣3)2=194. 当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P= (S≠0),这个函数的图象大致是( )A、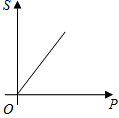 B、
B、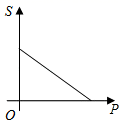 C、
C、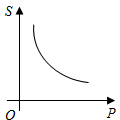 D、
D、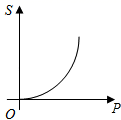 5. 在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个A、10 B、15 C、20 D、256. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人7. 如图,菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=6,BD=8,则OE长为( )
5. 在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个A、10 B、15 C、20 D、256. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人7. 如图,菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=6,BD=8,则OE长为( )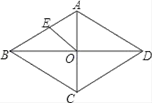 A、3 B、5 C、2.5 D、48. 如图, 中, ,若 , ,则 边的长是( )
A、3 B、5 C、2.5 D、48. 如图, 中, ,若 , ,则 边的长是( )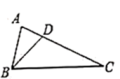 A、2 B、4 C、6 D、89. 下列结论中,错误的有:( )
A、2 B、4 C、6 D、89. 下列结论中,错误的有:( )①所有的菱形都相似;②放大镜下的图形与原图形不一定相似;
③等边三角形都相似;④有一个角为110度的两个等腰三角形相似;⑤所有的矩形不一定相似.
A、1个 B、2个 C、3个 D、4个10. 将n个边长都为1cm的正方形按如图所示的方法摆放,点A1 , A2 , …,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )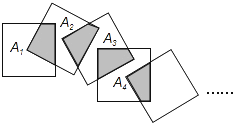 A、cm2 B、cm2 C、cm2 D、( )ncm2
A、cm2 B、cm2 C、cm2 D、( )ncm2二、填空题
-
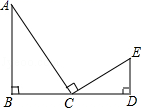
11. 若两个相似三角形的周长比为2:3,则它们的面积比是 .12. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是 .13. 从1,2,﹣3三个数中,随机抽取两个数相乘,积是偶数的概率是.14. 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=.
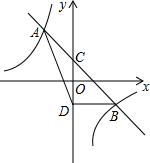
 15. 小亮在上午8时,9时30分,10时,12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为 .16. 若顺次连接四边形ABCD各边中点所得四边形为矩形,则四边形ABCD的对角线AC、BD之间的关系为.17. 如图,点B是反比例函数y= (x>0)的图象上任意一点,AB∥x轴并交反比例函数y=﹣ (x<0)的图象于点A,以AB为边作平行四边形ABCD,其中C、D在x轴上,则平行四边形ABCD的面积为.
15. 小亮在上午8时,9时30分,10时,12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为 .16. 若顺次连接四边形ABCD各边中点所得四边形为矩形,则四边形ABCD的对角线AC、BD之间的关系为.17. 如图,点B是反比例函数y= (x>0)的图象上任意一点,AB∥x轴并交反比例函数y=﹣ (x<0)的图象于点A,以AB为边作平行四边形ABCD,其中C、D在x轴上,则平行四边形ABCD的面积为.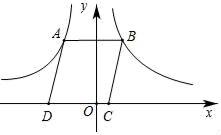 18. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF= S△ABF , 其中正确的结论有个.
18. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF= S△ABF , 其中正确的结论有个.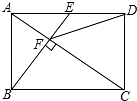
三、解答题
-
19. 用恰当的方法解下列方程.(1)、2x2﹣3x﹣1=0(2)、x2+2=2 x20. 如图,身高1.6米的小明站在距路灯底部O点10米的点A处,他的身高(线段AB)在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
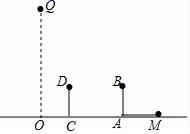 (1)、在OQ上画出表示路灯灯泡位置的点P;(2)、小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;(3)、若AM=2.5米,求路灯灯泡P到地面的距离.21. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)、在OQ上画出表示路灯灯泡位置的点P;(2)、小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;(3)、若AM=2.5米,求路灯灯泡P到地面的距离.21. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).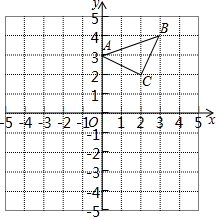
( 1 )画出△ABC向下平移4个单位长度得到的△A1B1C1;
( 2 )以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1;
(3)△A2B2C2的面积是 ▲ 平方单位.22. 如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE. 23. 在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为多少cm?
23. 在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为多少cm?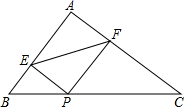 24. 有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看(1)、求甲选择A部电影的概率;(2)、求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)25. 2013年,东营市某楼盘以每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.(1)、求平均每年下调的百分率.
24. 有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看(1)、求甲选择A部电影的概率;(2)、求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)25. 2013年,东营市某楼盘以每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.(1)、求平均每年下调的百分率.
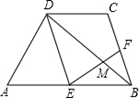
(2)、假设2016年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)26. 同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC , ∠ACF=∠ACB的方法得到四边形AECF(如图).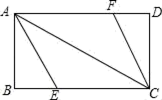 (1)、证明:四边形AECF是菱形;(2)、求菱形AECF的面积.
(1)、证明:四边形AECF是菱形;(2)、求菱形AECF的面积.