甘肃省定西市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-12-31 类型:期末考试
一、单选题
-
1. 下列四幅图案,在设计中用到了中心对称的图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是必然事件的是( )A、明天太阳从西边出来 B、打开电视,正在播放《新闻联播》 C、兰州是甘肃的省会 D、小明跑完 所用的时间为 分钟3. 一元二次方程3x2﹣x﹣2=0的二次项系数是3,它的一次项系数是( )A、﹣1 B、﹣2 C、1 D、04. 抛物线 的顶点坐标为( )A、(3,1) B、( ,1) C、(1,3) D、(1, )5. 已知 的半径为 ,点 的坐标为 ,点 的坐标为 ,则点 与 的位置关系是( )A、点 在 外 B、点 在 上 C、点 在 内 D、不能确定6. 如图,将 绕点 按逆时针方向旋转 后得到 ,若 ,则 的度数为( )
2. 下列事件中,是必然事件的是( )A、明天太阳从西边出来 B、打开电视,正在播放《新闻联播》 C、兰州是甘肃的省会 D、小明跑完 所用的时间为 分钟3. 一元二次方程3x2﹣x﹣2=0的二次项系数是3,它的一次项系数是( )A、﹣1 B、﹣2 C、1 D、04. 抛物线 的顶点坐标为( )A、(3,1) B、( ,1) C、(1,3) D、(1, )5. 已知 的半径为 ,点 的坐标为 ,点 的坐标为 ,则点 与 的位置关系是( )A、点 在 外 B、点 在 上 C、点 在 内 D、不能确定6. 如图,将 绕点 按逆时针方向旋转 后得到 ,若 ,则 的度数为( )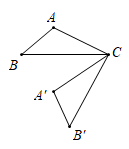 A、 B、 C、 D、7. 关于抛物线 的说法中,正确的是( )A、开口向下 B、与 轴的交点在 轴的下方 C、与 轴没有交点 D、 随 的增大而减小8. 已知关于 的一元二次方程 有两个实数根 , ,则代数式 的值为( )A、 B、 C、 D、9. 如图, 的外接圆 的半径是 .若 ,则 的长为( )
A、 B、 C、 D、7. 关于抛物线 的说法中,正确的是( )A、开口向下 B、与 轴的交点在 轴的下方 C、与 轴没有交点 D、 随 的增大而减小8. 已知关于 的一元二次方程 有两个实数根 , ,则代数式 的值为( )A、 B、 C、 D、9. 如图, 的外接圆 的半径是 .若 ,则 的长为( )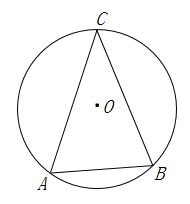 A、 B、 C、 D、10. 如图,这是二次函数 的图象,则 的值等于( )
A、 B、 C、 D、10. 如图,这是二次函数 的图象,则 的值等于( )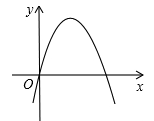 A、3 B、2 C、-2 D、-3
A、3 B、2 C、-2 D、-3二、填空题
-
11. 如图, 与 关于点 成中心对称,若 ,则 .
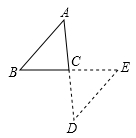 12. 在单词 (数学)中任意选择一个字母,选中字母“a”的概率为 .13. 一个正多边形的每个外角都等于 ,那么这个正多边形的中心角为.14. 将抛物线 先向右平移1个单位,再向下平移2个单位,所得到的抛物线的函数解析式是.15. 已知关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是.16. 如图,把直角三角板的直角顶点 放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点 、 .量得 , ,则该圆玻璃镜的半径是 .
12. 在单词 (数学)中任意选择一个字母,选中字母“a”的概率为 .13. 一个正多边形的每个外角都等于 ,那么这个正多边形的中心角为.14. 将抛物线 先向右平移1个单位,再向下平移2个单位,所得到的抛物线的函数解析式是.15. 已知关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是.16. 如图,把直角三角板的直角顶点 放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点 、 .量得 , ,则该圆玻璃镜的半径是 .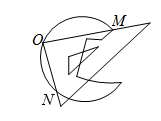 17. 某厂前年缴税 万元,今年缴税 万元, 如果该厂缴税的年平均增长率为 ,那么可列方程为.18. 观察下列各数:0,3,8,15,24,……按此规律写出的第10个数是 , 第 个数是.
17. 某厂前年缴税 万元,今年缴税 万元, 如果该厂缴税的年平均增长率为 ,那么可列方程为.18. 观察下列各数:0,3,8,15,24,……按此规律写出的第10个数是 , 第 个数是.三、解答题
-
19. 解方程:3x(x+1)=3x+3.
20. 如图,每个小正方形的边长为1个单位长度,请作出 关于原点对称的 ,并写出点 的坐标.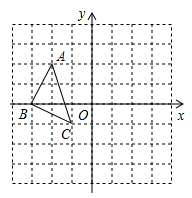 21. 如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.判断△ABC的形状,并证明你的结论;
21. 如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.判断△ABC的形状,并证明你的结论;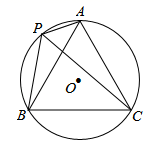 22. 一个不透明的口袋中装有4张卡片,卡片上分别标有数字1、-2、-3、4,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.(1)、求小芳抽到负数的概率;(2)、若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率.23. 如图,半圆 的直径 ,将半圆 绕点 顺时针旋转 得到半圆 ,半圆 与 交于点 .
22. 一个不透明的口袋中装有4张卡片,卡片上分别标有数字1、-2、-3、4,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.(1)、求小芳抽到负数的概率;(2)、若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率.23. 如图,半圆 的直径 ,将半圆 绕点 顺时针旋转 得到半圆 ,半圆 与 交于点 . (1)、求 的长;(2)、求图中阴影部分的面积.(结果保留 )24. 在直角坐标平面内,某二次函数图象的顶点为 ,且经过点 .(1)、求该二次函数的解析式;(2)、求直线y=-x-1与该二次函数图象的交点坐标.25. 如图, 是 的直径, , ,连接 交 于点 .
(1)、求 的长;(2)、求图中阴影部分的面积.(结果保留 )24. 在直角坐标平面内,某二次函数图象的顶点为 ,且经过点 .(1)、求该二次函数的解析式;(2)、求直线y=-x-1与该二次函数图象的交点坐标.25. 如图, 是 的直径, , ,连接 交 于点 .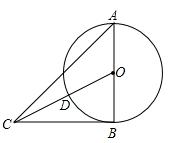 (1)、求证: 是 的切线;(2)、若 ,求 的长.26. 某日王老师佩戴运动手环进行快走锻炼两次锻炼后数据如下表,与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为 .注:步数 平均步长 距离.
(1)、求证: 是 的切线;(2)、若 ,求 的长.26. 某日王老师佩戴运动手环进行快走锻炼两次锻炼后数据如下表,与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为 .注:步数 平均步长 距离.项目
第一次锻炼
第二次锻炼
步数(步)
①_______
平均步长(米/步)
②_______
距离(米)
(1)、根据题意完成表格;(2)、求 .27. 如图,抛物线 与 轴交于 、 两点,与 轴交于点 ,且 , .
 (1)、求抛物线的解析式;(2)、已知抛物线上点 的横坐标为 ,在抛物线的对称轴上是否存在点 ,使得 的周长最小?若存在,求出点 的坐标;若不存在,请说明理由.28. 问题背景:如图1,在 中, , , ,四边形 是正方形,求图中阴影部分的面积.
(1)、求抛物线的解析式;(2)、已知抛物线上点 的横坐标为 ,在抛物线的对称轴上是否存在点 ,使得 的周长最小?若存在,求出点 的坐标;若不存在,请说明理由.28. 问题背景:如图1,在 中, , , ,四边形 是正方形,求图中阴影部分的面积.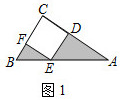 (1)、发现:如图2,小芳发现,只要将 绕点 逆时针旋转一定的角度到达 ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为;(直接写出答案)
(1)、发现:如图2,小芳发现,只要将 绕点 逆时针旋转一定的角度到达 ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为;(直接写出答案)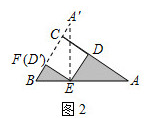 (2)、应用:如图3,在四边形 中, , , 于点 ,若四边形 的面积为16,试求出 的长;
(2)、应用:如图3,在四边形 中, , , 于点 ,若四边形 的面积为16,试求出 的长;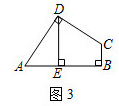 (3)、拓展:如图4,在四边形 中, , , ,以 为顶点作 为 角,角的两边分别交 , 于 , 两点,连接 ,请直接写出线段 , , 之间的数量关系.
(3)、拓展:如图4,在四边形 中, , , ,以 为顶点作 为 角,角的两边分别交 , 于 , 两点,连接 ,请直接写出线段 , , 之间的数量关系.