甘肃省临洮县2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-12-31 类型：期末考试

进入出卷网下载

一、单选题

1. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（　　）

A、 B、 C、 D、

查看试题解析
2. 随着电子技术的不断进步，电子元件的尺寸大幅缩小，电脑芯片上某电子元件大约只有 $0.000000645 m m^{2}$ ，这个数用科学记数法表示为（）

A、 $6.45 \times 10^{6}$ B、 $6.45 \times 10^{7}$ C、 $6.45 \times 10^{- 6}$ D、 $6.45 \times 10^{- 7}$

查看试题解析
3. 如图，以正方形ABCD的中心为原点建立平面直角坐标系，点A的坐标为（2，2），则点C的坐标为（）

A、（2，2） B、（﹣2，2） C、（﹣2，﹣2） D、（2，﹣2）

查看试题解析
4. 如图，在 $Δ A B C$ 中，AB=AC，D是BC的中点，下列结论不正确的是（）

A、AD $⊥$ BC B、∠B=∠C C、AB=2BD D、AD平分∠BAC

查看试题解析
5. 若长方形的长为 (4a²-2a +1) ，宽为 (2a +1) ，则这个长方形的面积为（）

A、8a³-4a²+2a-1 B、8a³-1 C、8a³+4a²-2a-1 D、8a³+1

查看试题解析
6. 如图，五边形 ABCDE 中，AB∥CD，则图中 x 的值是（）

A、75° B、65° C、60° D、55°

查看试题解析
7. 已知 $m$ 、 $n$ 均为正整数，且 $2 m + 3 n = 5$ ，则 $4^{m} \cdot 8^{n} =$ （）

A、 $16$ B、 $25$ C、 $32$ D、 $64$

查看试题解析
8.
如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（　　）

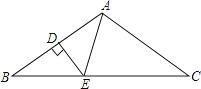A、80° B、60° C、50° D、40°

查看试题解析
9. “十一”旅游黄金周期间，几名同学包租一辆面包车前往“红螺寺”游玩，面包车的租价为180元，出发时，又增加了2名学生，结果每个同学比原来少分担3元车费，原参加游玩的同学为x人，则可得方程（）

A、 $\frac{180}{x}$ - $\frac{180}{x + 2}$ =3 B、 $\frac{180}{x + 2}$ - $\frac{180}{x}$ =3 C、 $\frac{180}{x}$ - $\frac{180}{x - 2}$ =3 D、 $\frac{180}{x - 2}$ - $\frac{180}{x}$ =3

查看试题解析
10. 如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S_△_ABC＝4cm² ，则S_阴影等于…（）

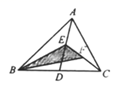A、2cm² B、1cm² C、 $\frac{1}{2}$ cm² D、 $\frac{1}{4}$ cm²

查看试题解析

二、填空题

11. 计算： ${(- 2)}^{0} \cdot 2^{- 3} =$ ， ${(8 a^{6} b^{3})}^{2} \div (- 2 a^{2} b) =$ .

查看试题解析
12. 一个多边形的每个外角都是36°，这个多边形是边形

查看试题解析
13. 因式分解： ${(a - b)}^{2} - 4 b^{2} =$ .

查看试题解析
14. 一个n边形的内角和为1080°，则n= ．

查看试题解析
15. 若分式 $\frac{| x | - 3}{x - 3}$ 的值为零，则x= ．

查看试题解析
16. 已知点A（m+3，2）与点B（1，n﹣1）关于y轴对称，则代数式（m+n）²⁰¹⁷的值为.

查看试题解析
17. 如图，已知 $∠ M O N = 30 °$ ，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ，…在射线ON上，点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ，…在射线OM上， $Δ A_{1} B_{1} A_{2}$ ， $Δ A_{2} B_{2} A_{3}$ ， $Δ A_{3} B_{3} A_{4}$ ，…均为等边三角形，若 $O A_{1} = 2$ ，则 $Δ A_{5} B_{5} A_{6}$ 的边长为.

查看试题解析

三、解答题

18. 计算：

(1)、 $(a - 2 b + 1) (a + 2 b + 1)$ ；

(2)、 ${(x + 2 y - 1)}^{2}$ .

查看试题解析
19. 分解因式：

(1)、 $a^{3} - a b^{2}$ ；

(2)、 $a^{2} + 6 a b + 9 b^{2}$ .

查看试题解析
20. 解方程：

(1)、 $\frac{1}{2 x} = \frac{2}{x + 3}$ ；

(2)、 $\frac{1 - x}{x - 2} + \frac{x + 3}{2 - x} = 1$ .

查看试题解析
21. 先化简，再求值：（1﹣ $\frac{1}{x + 1}$ ）÷ $\frac{x - 2}{x + 1}$ ，从﹣1，2，3中选择一个适当的数作为x值代入．

查看试题解析
22. 已知：∠AOB和两点C、D，求作一点P，使PC=PD，且点P到∠AOB的两边的距离相等．（要求：用尺规作图，保留作图痕迹，不写作法，不要求证明）

查看试题解析
23. 已知（x²+mx+n）（x+1）的结果中不含x²项和x项，求m，n的值.

查看试题解析
24. 在“母亲节”前夕，某花店用16000元购进第一批礼盒鲜花，上市后很快预售一空．根据市场需求情况，该花店又用7500元购进第二批礼盒鲜花．已知第二批所购鲜花的盒数是第一批所购鲜花的 $\frac{1}{2}$ ，且每盒鲜花的进价比第一批的进价少10元．问第二批鲜花每盒的进价是多少元？

查看试题解析
25. 如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，DE=1cm，求BD的长.

查看试题解析
26. 如图，等边 $Δ A B C$ 的边长为 $4$ ， $A D$ 是 $B C$ 边上的中线， $F$ 是 $A D$ 边上的动点， $E$ 是 $A C$ 边上一点，若 $A E = 2$ ，当 $E F + C F$ 取得最小值时，则 $∠ E C F$ 的度数为多少？

查看试题解析
27. 如图， $△ A B C$ 中， $A B = A C ， ∠ A = 108^{\circ}$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于 $D$ 点.
求证：BC=AC+CD.

查看试题解析