甘肃省白银市会宁县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-31 类型:期末考试
一、单选题
-
1. 判断以下各组线段为边作三角形,可以构成直角三角形的是( )A、6,15,17 B、7,12,15 C、13,15,20 D、7,24,252. 下列说法正确的有( )
①无理数是无限小数;②无限小数是无理数;③开方开不尽的数是无理数;④两个无理数的和一定是无理数;⑤无理数的平方一定是有理数.
A、1个 B、2个 C、3个 D、4个3. 平方根等于它本身的数是( )A、0 B、1,0 C、0, 1 ,-1 D、0, -14. 下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=3:4:5 B、∠A:∠B:∠C=3:4:5 C、∠A+∠B=∠C D、a:b:c=1:2:5. 一次函数 满足
满足 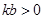 ,且
,且  随 x 的增大而减小,则此函数的图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,直角坐标系中四边形的面积是( )
随 x 的增大而减小,则此函数的图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,直角坐标系中四边形的面积是( ) A、4 B、5.5 C、4.5 D、57. 将平面直角坐标系内某个图形上各点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的关系是( )A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、两图形重合8. 下列各点在函数y=1-2x的图象上的是( )A、 B、 C、 D、9. 已知一次函数 ,函数值 随自变量 的增大而减小,那么m 的取值范围是( )A、 B、 C、 D、10. 一辆客车从霍山开往合肥,设客车出发th后与合肥的距离为skm , 则下列图象中能大致反映s与t之间函数关系的是( )A、
A、4 B、5.5 C、4.5 D、57. 将平面直角坐标系内某个图形上各点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的关系是( )A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、两图形重合8. 下列各点在函数y=1-2x的图象上的是( )A、 B、 C、 D、9. 已知一次函数 ,函数值 随自变量 的增大而减小,那么m 的取值范围是( )A、 B、 C、 D、10. 一辆客车从霍山开往合肥,设客车出发th后与合肥的距离为skm , 则下列图象中能大致反映s与t之间函数关系的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 关于x,y的方程组 的解是 ,其中y的值被盖住了.不过仍能求出m,则m的值是.12. 如图,长方体的长为 ,宽为 ,高为 ,点 离点 的距离为 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是。
 13. 如图直线a,b交于点A,则以点A的坐标为解的方程组是.
13. 如图直线a,b交于点A,则以点A的坐标为解的方程组是. 14. 某种大米的单价是2.4元/千克,当购买x千克大米时,花费为y元,则x与y的函数关系式是.15. 甲、乙俩射击运动员进行10次射击,甲的成绩是7,7,8,9,8,9,10,9,9,9,乙的成绩如图所示.则甲、乙射击成绩的方差之间关系是
14. 某种大米的单价是2.4元/千克,当购买x千克大米时,花费为y元,则x与y的函数关系式是.15. 甲、乙俩射击运动员进行10次射击,甲的成绩是7,7,8,9,8,9,10,9,9,9,乙的成绩如图所示.则甲、乙射击成绩的方差之间关系是
 (填“<”,“=”,“>”).
(填“<”,“=”,“>”).
 16. 如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=度.
16. 如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=度. 17. 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2 , 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 , 以此类推……则正方形OB2019B2020C2020的顶点B2020的坐标是 .
17. 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2 , 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 , 以此类推……则正方形OB2019B2020C2020的顶点B2020的坐标是 .
三、解答题
-
18. 计算:(1)、 ;(2)、( -2 )× -6 ;(3)、 ;(4)、 .19. 某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
西瓜质量(单位:千克)
5.4
5.3
5.0
4.8
4.4
4.0
西瓜数量(单位:个)
1
2
3
2
1
1
(1)、这10个西瓜质量的众数和中位数分别是和;(2)、计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?20. 如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F. 21. 在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上。在建立平面直角坐标系后,点B的坐标为(-1,2).
21. 在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上。在建立平面直角坐标系后,点B的坐标为(-1,2). (1)、把△ABC向下平移8个单位后得到对应的△ ,画出△ ,并写出 坐标;(2)、以原点O为对称中心,画出与△ 关于原点O对称的△ ,并写出点 的坐标.22. 如图,长方形 中 ∥ ,边 , .将此长方形沿 折叠,使点 与点 重合,点 落在点 处.
(1)、把△ABC向下平移8个单位后得到对应的△ ,画出△ ,并写出 坐标;(2)、以原点O为对称中心,画出与△ 关于原点O对称的△ ,并写出点 的坐标.22. 如图,长方形 中 ∥ ,边 , .将此长方形沿 折叠,使点 与点 重合,点 落在点 处. (1)、试判断 的形状,并说明理由;(2)、求 的面积.23. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动.
(1)、试判断 的形状,并说明理由;(2)、求 的面积.23. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动. (1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、当△ONC的面积是△OAC面积的 时,求出这时点N的坐标.24. 某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.(1)、求这两种品牌计算器的单价;(2)、学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;(3)、当需要购买50个计算器时,买哪种品牌的计算器更合算?
(1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、当△ONC的面积是△OAC面积的 时,求出这时点N的坐标.24. 某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.(1)、求这两种品牌计算器的单价;(2)、学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;(3)、当需要购买50个计算器时,买哪种品牌的计算器更合算?