2016年山东省济宁市中考数学试卷

试卷更新日期：2016-07-01 类型：中考真卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求

1. 在：0，﹣2，1， $\frac{1}{2}$ 这四个数中，最小的数是（　　）

A、0 B、﹣2 C、1 D、 $\frac{1}{2}$

查看试题解析
2. 下列计算正确的是（　　）

A、x²•x³=x⁵ B、x⁶+x⁶=x¹² C、（x²）³=x⁵ D、x^﹣¹=x

查看试题解析
3.
如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1=55°，那么∠2的度数是（　　）

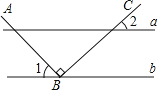A、20° B、30° C、35° D、50°

查看试题解析
4.
如图，几何体是由3个大小完全一样的正方体组成的，它的左视图是（　　）

A、 B、 C、 D、

查看试题解析
5.
如图，在⊙O中， $\overset{\land}{A B}$ = $\overset{\land}{A C}$ ，∠AOB=40°，则∠ADC的度数是（　　）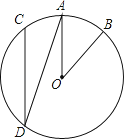

A、40° B、30° C、20° D、15°

查看试题解析
6. 已知x﹣2y=3，那么代数式3﹣2x+4y的值是（　　）

A、﹣3 B、3 C、6 D、9

查看试题解析
7.
如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是（　　）

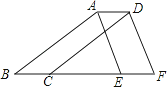A、16cm B、18cm C、20cm D、21cm

查看试题解析
8. 在学校开展的“争做最优秀中学生”的一次演讲比赛中，编号1，2，3，4，5的五位同学最后成绩如下表所示：
参赛者编号
1
2
3
4
5
成绩/分
96
88
86
93
86
那么这五位同学演讲成绩的众数与中位数依次是（　　）

A、96，88， B、86，86 C、88，86 D、86，88

查看试题解析
9.
如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（　　）

A、 $\frac{6}{13}$ B、 $\frac{5}{13}$ C、 $\frac{4}{13}$ D、 $\frac{3}{13}$

查看试题解析
10.
如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB= $\frac{4}{5}$ ，反比例函数y= $\frac{48}{x}$ 在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于（　　）

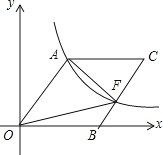A、60 B、80 C、30 D、40

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分

11. 若式子 $\sqrt{x - 1}$ 有意义，则实数x的取值范围是．

查看试题解析
12.
如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：，使△AEH≌△CEB．

查看试题解析
13.
如图，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，那么 $\frac{B C}{C E}$ 的值等于．

查看试题解析
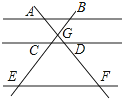14. 已知A，B两地相距160km，一辆汽车从A地到B地的速度比原来提高了25%，结果比原来提前0.4h到达，这辆汽车原来的速度是km/h．

查看试题解析
15. 按一定规律排列的一列数： $\frac{1}{2}$ ，1，1，□， $\frac{3}{11}$ ， $\frac{11}{13}$ ， $\frac{13}{17}$ ，…请你仔细观察，按照此规律方框内的数字应为．

查看试题解析

三、解答题：本大题共7小题，共55分

16. 先化简，再求值：a（a﹣2b）+（a+b）² ，其中a=﹣1，b= $\sqrt{2}$ ．

查看试题解析
17.
2016年6月15日是父亲节，某商店老板统计了这四年父亲节当天剃须刀销售情况，以下是根据该商店剃须刀销售的相关数据所绘制统计图的一部分．

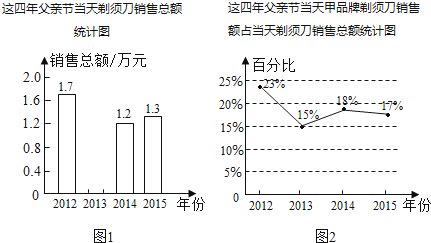
请根据图1、图2解答下列问题：

(1)、近四年父亲节当天剃须刀销售总额一共是5.8万元，请将图1中的统计图补充完整；

(2)、计算该店2015年父亲节当天甲品牌剃须刀的销售额．

查看试题解析
18.
某地的一座人行天桥如图所示，天桥高为6米，坡面BC的坡度为1：1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1： $\sqrt{3}$ ．

(1)、求新坡面的坡角a；

(2)、原天桥底部正前方8米处（PB的长）的文化墙PM是否需要拆桥？请说明理由．

查看试题解析
19. 某地2014年为做好“精准扶贫”，授入资金1280万元用于异地安置，并规划投入资金逐年增加，2016年在2014年的基础上增加投入资金1600万元．

(1)、从2014年到2016年，该地投入异地安置资金的年平均增长率为多少？

(2)、在2016年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天补助5元，按租房400天计算，试求今年该地至少有多少户享受到优先搬迁租房奖励？

查看试题解析
20.
如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO．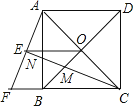

(1)、已知BD= $\sqrt{2}$ ，求正方形ABCD的边长；

(2)、猜想线段EM与CN的数量关系并加以证明．

查看试题解析
21. 已知点P（x₀ ， y₀）和直线y=kx+b，则点P到直线y=kx+b的距离证明可用公式d= $\frac{| k x_{0} - y_{0} + b |}{\sqrt{1 + k^{2}}}$ 计算．
例如：求点P（﹣1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（﹣1，2）到直线y=3x+7的距离为：d= $\frac{| k x_{0} - y_{0} + b |}{\sqrt{1 + k^{2}}}$ = $\frac{| 3 \times (- 1) - 2 + 7 |}{\sqrt{1 + k^{2}}}$ = $\frac{2}{\sqrt{10}}$ = $\frac{\sqrt{10}}{5}$ ．

根据以上材料，解答下列问题：

(1)、求点P（1，﹣1）到直线y=x﹣1的距离；

(2)、已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y= $\sqrt{3}$ x+9的位置关系并说明理由；

(3)、已知直线y=﹣2x+4与y=﹣2x﹣6平行，求这两条直线之间的距离．

查看试题解析
22.
如图，已知抛物线m：y=ax²﹣6ax+c（a＞0）的顶点A在x轴上，并过点B（0，1），直线n：y=﹣ $\frac{1}{2}$ x+ $\frac{7}{2}$ 与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（﹣7，7）．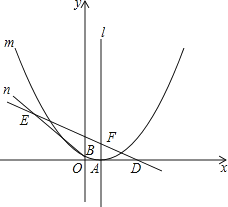

(1)、求抛物线m的解析式；

(2)、P是l上的一个动点，若以B，E，P为顶点的三角形的周长最小，求点P的坐标；

(3)、抛物线m上是否存在一动点Q，使以线段FQ为直径的圆恰好经过点D？若存在，求点Q的坐标；若不存在，请说明理由．

查看试题解析

参赛者编号	1	2	3	4	5
成绩/分	96	88	86	93	86