初中数学浙教版八年级上学期期末复习专题10——一次函数的图像与简单应用
试卷更新日期:2020-12-31 类型:复习试卷
一、单选题
-
1. P1(x1 , y1),P2(x2 , y2)是正比例函数y=﹣x图象上两点,则下列正确的是( )A、y1>y2 B、y1<y2 C、当x1<x2时,y1<y2 D、当x1>x2时,y1<y22. 已知函数y=kx+b的图象如图所示,则y=-2kx+b的图象可能是( )
 A、
A、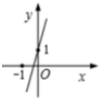 B、
B、 C、
C、 D、
D、 3. 已知正比例函数 ,且y随x的增大而减少,则直线 的图像是( )A、
3. 已知正比例函数 ,且y随x的增大而减少,则直线 的图像是( )A、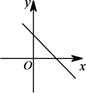 B、
B、 C、
C、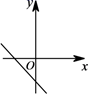 D、
D、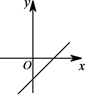 4. 如图,已知函数y=kx(k≠0)和y=ax+b(a≠0)的图象交于点P(-3,1),则关于x的不等式kx≥ax+b的解集是( )
4. 如图,已知函数y=kx(k≠0)和y=ax+b(a≠0)的图象交于点P(-3,1),则关于x的不等式kx≥ax+b的解集是( )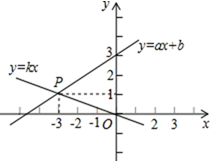 A、 B、 C、 D、5. 如图,是在同一坐标系内作出的一条函数的图象l1 , l2 , 设y=k1x+b1 , y=k2x+b2 , 则方程组 的解是( ).
A、 B、 C、 D、5. 如图,是在同一坐标系内作出的一条函数的图象l1 , l2 , 设y=k1x+b1 , y=k2x+b2 , 则方程组 的解是( ).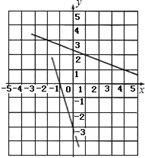 A、 B、 C、 D、不能确定6. 已知一次函数的图象与直线y=-2x+1平行,且过点(8,2)那么此一次函数的解析式为( )A、y=2x-14 B、y=-2x+18 C、y=4x D、y=-2x+127. 在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
A、 B、 C、 D、不能确定6. 已知一次函数的图象与直线y=-2x+1平行,且过点(8,2)那么此一次函数的解析式为( )A、y=2x-14 B、y=-2x+18 C、y=4x D、y=-2x+127. 在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( ) A、小莹的速度随时间的增大而增大 B、小梅的平均速度比小莹的平均速度大 C、在起跑后180秒时,两人相遇 D、在起跑后50秒时,小梅在小莹的前面8. 无论m为何实数,直线 与 的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 为了改善生态环境,政府决定绿化荒地,计划第一年先植树2万亩,以后每年都植树2.5万亩,则植树的总面积 (万亩)与时间 (年)的函数关系式是( )A、 B、 C、 D、10. 如图, 过点A(2,0)和点B(0,-1),则方程 解是( )
A、小莹的速度随时间的增大而增大 B、小梅的平均速度比小莹的平均速度大 C、在起跑后180秒时,两人相遇 D、在起跑后50秒时,小梅在小莹的前面8. 无论m为何实数,直线 与 的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 为了改善生态环境,政府决定绿化荒地,计划第一年先植树2万亩,以后每年都植树2.5万亩,则植树的总面积 (万亩)与时间 (年)的函数关系式是( )A、 B、 C、 D、10. 如图, 过点A(2,0)和点B(0,-1),则方程 解是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
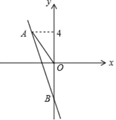
11. 一次函数y=2x-4的图象与x轴的交点坐标是.12. 若点A(-5,y1),B(-2,y2)都在一次函数 的图像上,则y1y2(填“>”或“<”).13. 将y=2x﹣3的图象向上平移2个单位长度得到的直线表达式为.14. 如图,点A(a,4)在一次函数y=-3x-5的图象上,图象与y轴的交点为B,那么△AOB的面积为
 15. 将长为30cm,宽为10cm的长方形白纸,按如图所示的方发粘合起来,粘合部分的宽为3cm.设x张白纸粘合后的总长度为ycm,则y与x的函数关系式.
15. 将长为30cm,宽为10cm的长方形白纸,按如图所示的方发粘合起来,粘合部分的宽为3cm.设x张白纸粘合后的总长度为ycm,则y与x的函数关系式. 16. 如图,已知函数y=ax+2与y=bx-3的图象交于点A(2,-1),则根据图象可得不等式ax>bx-5的解集是.
16. 如图,已知函数y=ax+2与y=bx-3的图象交于点A(2,-1),则根据图象可得不等式ax>bx-5的解集是.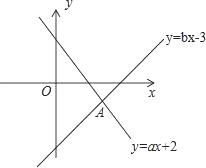
三、综合题
-
17. 如图,一次函数y x+6与坐标轴交于A、B两点,求点A、B的坐标.
 18. 如图,正比例函数y=kx的图象经过点A,点A在第二象限.过点A作AH⊥x
18. 如图,正比例函数y=kx的图象经过点A,点A在第二象限.过点A作AH⊥x轴,垂足为H.已知点A的横坐标为﹣3,且△AOH的面积4.5.
 (1)、求该正比例函数的解析式.(2)、将正比例函数y=kx向下平移,使其恰好经过点H,求平移后的函数解析式.19. 某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
(1)、求该正比例函数的解析式.(2)、将正比例函数y=kx向下平移,使其恰好经过点H,求平移后的函数解析式.19. 某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.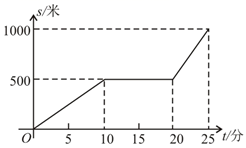 (1)、学校离他家米,从出发到学校,王老师共用了分钟;王老师吃早餐用了分钟?(2)、观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?(3)、求出王老师吃完早餐后的平均速度是多少?20. 我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:
(1)、学校离他家米,从出发到学校,王老师共用了分钟;王老师吃早餐用了分钟?(2)、观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?(3)、求出王老师吃完早餐后的平均速度是多少?20. 我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:品种
购买价(元/棵)
成活率
甲
20
90%
乙
32
95%
设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1)、设y与x之间的函数关系式,并写出自变量x的取值范围;
(2)、承包商要获得不低于中标价16%的利润,应如何选购树苗?(3)、政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?21. 如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a),l1与y轴交于点C,l2与x轴交于点A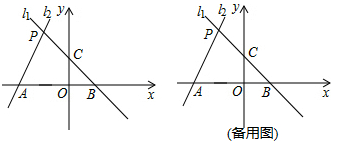 (1)、求a的值及直线l1的解析式。(2)、求四边形PAOC的面积。(3)、在x轴上方有一动直线平行于x轴,分别与l1 , l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由。
(1)、求a的值及直线l1的解析式。(2)、求四边形PAOC的面积。(3)、在x轴上方有一动直线平行于x轴,分别与l1 , l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由。