2016年安徽省中考数学试卷

试卷更新日期：2016-07-01 类型：中考真卷

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）

1. ﹣2的绝对值是（　　）

A、﹣2 B、2 C、±2 D、 $\frac{1}{2}$

查看试题解析
2. 计算a¹⁰÷a²（a≠0）的结果是（　　）

A、a⁵ B、a^﹣⁵ C、a⁸ D、a^﹣⁸

查看试题解析
3. 2016年3月份我省农产品实现出口额8362万美元，其中8362万用科学记数法表示为（　　）

A、8.362×10⁷ B、83.62×10⁶ C、0.8362×10⁸ D、8.362×10⁸

查看试题解析
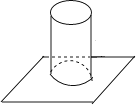
4.
如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（　　）

A、 B、 C、 D、

查看试题解析
5. 方程 $\frac{2 x + 1}{x - 1}$ =3的解是（　　）

A、﹣ $\frac{4}{5}$ B、 $\frac{4}{5}$ C、﹣4 D、4

查看试题解析
6. 2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（　　）

A、b=a（1+8.9%+9.5%） B、b=a（1+8.9%×9.5%） C、b=a（1+8.9%）（1+9.5%） D、b=a（1+8.9%）²（1+9.5%）

查看试题解析
7.
自来水公司调查了若干用户的月用水量x（单位：吨），按月用水量将用户分成A、B、C、D、E五组进行统计，并制作了如图所示的扇形统计图．已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有（　　）
组别
月用水量x（单位：吨）
A
0≤x＜3
B
3≤x＜6
C
6≤x＜9
D
9≤x＜12
E
x≥12

A、18户 B、20户 C、22户 D、24户

查看试题解析
8.
如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为（　　）

A、4 B、4 $\sqrt{2}$ C、6 D、4 $\sqrt{3}$

查看试题解析
9. 一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程y（千米）与时间x（小时）函数关系的图象是（　　）

A、 B、 C、 D、

查看试题解析
10.
如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（　　）

A、 $\frac{3}{2}$ B、2 C、 $\frac{8 \sqrt{13}}{13}$ D、 $\frac{12 \sqrt{13}}{13}$

查看试题解析

二、填空题（本大题共4小题，每小题5分，满分20分）

11. 不等式x﹣2≥1的解集是．

查看试题解析
12. 因式分解：a³﹣a= ．

查看试题解析
13.
如图，已知⊙O的半径为2，A为⊙O外一点，过点A作⊙O的一条切线AB，切点是B，AO的延长线交⊙O于点C，若∠BAC=30°，则劣弧 $\overset{\land}{B C}$ 的长为．

查看试题解析
14.
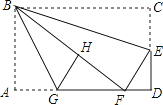
如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
①∠EBG=45°；②△DEF∽△ABG；③S_△_ABG= $\frac{3}{2}$ S_△_FGH；④AG+DF=FG．
其中正确的是．（把所有正确结论的序号都选上）

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 计算：（﹣2016）⁰+ $\sqrt[3]{- 8}$ +tan45°．

查看试题解析
16. 解方程：x²﹣2x=4．

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17.
如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC．

(1)、试在图中标出点D，并画出该四边形的另两条边；

(2)、将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′．

查看试题解析
18. 按要求回答问题

(1)、
观察下列图形与等式的关系，并填空：

(2)、
观察下图，根据（1）中结论，计算图中黑球的个数，用含有n的代数式填空：

1+3+5+…+（2n﹣1）+（）+（2n﹣1）+…+5+3+1= ．

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

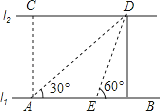
19.
如图，河的两岸l₁与l₂相互平行，A、B是l₁上的两点，C、D是l₂上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．

查看试题解析
20.
如图，一次函数y=kx+b的图象分别与反比例函数y= $\frac{a}{x}$ 的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．

(1)、求函数y=kx+b和y= $\frac{a}{x}$ 的表达式；

(2)、已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．

查看试题解析

六、（本大题满分12分）

21. 一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．

(1)、写出按上述规定得到所有可能的两位数；

(2)、从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．

查看试题解析

七、（本大题满分12分）

22.
如图，二次函数y=ax²+bx的图象经过点A（2，4）与B（6，0）．

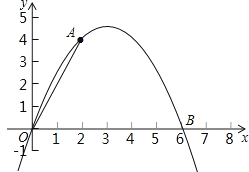(1)、求a，b的值；

(2)、点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．

查看试题解析

八、（本大题满分14分）

23.
如图1，A，B分别在射线OA，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．

(1)、求证：△PCE≌△EDQ；

(2)、延长PC，QD交于点R．
①如图1，若∠MON=150°，求证：△ABR为等边三角形；
②如图3，若△ARB∽△PEQ，求∠MON大小和 $\frac{A B}{P Q}$ 的值．

查看试题解析

组别	月用水量x（单位：吨）
A	0≤x＜3
B	3≤x＜6
C	6≤x＜9
D	9≤x＜12
E	x≥12