人教A版(2019) 必修一 5.6 函数y=Asin(wx+φ)
试卷更新日期:2020-12-31 类型:同步测试
一、单选题
-
1. 已知函数 的部分图象如图所示.则 的解析式为( ).
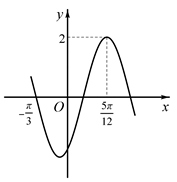 A、 B、 C、 D、2. 若将函数 的图象向左平移 个单位长度后.得到的函数图象关于 对称.则函数 在 上的最小值是( ).A、-1 B、 C、 D、03. 将函数 图象上每一点的横坐标变为原来的2倍,再将图像向左平移 个单位长度,得到函数 的图象,则函数 图象的一个对称中心为( )A、 B、 C、 D、4. 为了得到函数 的图象,可将函数 的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位5. 把正弦函数 图象上所有的点向左平移 个长度单位,再把所得函数图象上所有的点的横坐标缩短到原来的 倍,得到的函数是( )A、 B、 C、 D、6. 已知曲线 ,则下面结论正确的是( )A、先将曲线 向左平移 个单位长度,再把所得的曲线上各点横坐标缩短为原来的 倍,纵坐标保持不变,便得到曲线 B、先将曲线 向右平移 个单位长度,再把所得的曲线上各点横坐标伸长为原来的2倍,纵坐标保持不变,便得到曲线 C、先将曲线 向左平移 个单位长度,再把所得的曲线上各点横坐标伸长为原来的2倍,纵坐标保持不变,便得到曲线 D、先将曲线 向右平移 个单位长度,再把所得的曲线上各点横坐标缩短为原来的 倍,纵坐标保持不变,便得到曲线7. 已知函数 的部分图象如图所示,则 的单调递增区间为( )
A、 B、 C、 D、2. 若将函数 的图象向左平移 个单位长度后.得到的函数图象关于 对称.则函数 在 上的最小值是( ).A、-1 B、 C、 D、03. 将函数 图象上每一点的横坐标变为原来的2倍,再将图像向左平移 个单位长度,得到函数 的图象,则函数 图象的一个对称中心为( )A、 B、 C、 D、4. 为了得到函数 的图象,可将函数 的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位5. 把正弦函数 图象上所有的点向左平移 个长度单位,再把所得函数图象上所有的点的横坐标缩短到原来的 倍,得到的函数是( )A、 B、 C、 D、6. 已知曲线 ,则下面结论正确的是( )A、先将曲线 向左平移 个单位长度,再把所得的曲线上各点横坐标缩短为原来的 倍,纵坐标保持不变,便得到曲线 B、先将曲线 向右平移 个单位长度,再把所得的曲线上各点横坐标伸长为原来的2倍,纵坐标保持不变,便得到曲线 C、先将曲线 向左平移 个单位长度,再把所得的曲线上各点横坐标伸长为原来的2倍,纵坐标保持不变,便得到曲线 D、先将曲线 向右平移 个单位长度,再把所得的曲线上各点横坐标缩短为原来的 倍,纵坐标保持不变,便得到曲线7. 已知函数 的部分图象如图所示,则 的单调递增区间为( ) A、 , B、 , C、 , D、 ,8. 若将函数 的图象向右平移 个单位长度后,所得图象的一个对称中心为( )A、 B、 C、 D、9. 已知函数f(x)=2sin(ωx+ )(ω>0)的图象在区间[0,1]上恰有3个最高点,则ω的取值范围为( )A、 B、 C、 D、10. 函数 (其中 , , )的图像如图所示,则使 成立的 的最小正值为( )
A、 , B、 , C、 , D、 ,8. 若将函数 的图象向右平移 个单位长度后,所得图象的一个对称中心为( )A、 B、 C、 D、9. 已知函数f(x)=2sin(ωx+ )(ω>0)的图象在区间[0,1]上恰有3个最高点,则ω的取值范围为( )A、 B、 C、 D、10. 函数 (其中 , , )的图像如图所示,则使 成立的 的最小正值为( ) A、 B、 C、 D、11. 已知函数 ( , )的部分图像如图所示,若存在 ,满足 ,则 ( )
A、 B、 C、 D、11. 已知函数 ( , )的部分图像如图所示,若存在 ,满足 ,则 ( ) A、 B、 C、 D、12. 已知函数 ,给出下列四个结论:
A、 B、 C、 D、12. 已知函数 ,给出下列四个结论:①函数 的最小正周期是 ;②函数 在区间 上是减函数;③函数 的图象关于直线 对称;④函数 的图象可由函数 的图象向左平移 个单位得到其中所有正确结论的编号是( )
A、①② B、①③ C、①②③ D、①③④13. 已知函数 的图象与直线 的三个相邻交点的横坐标分别是2,4,8,则 的单调递减区间是( )A、 , B、 , C、 , D、 ,14. 已知 , 为函数 的图象与 轴的两个相邻交点的横坐标,将 的图象向左平移 个单位得到 的图象,A,B,C为两个函数图象的交点,则 面积的最小值为( ).A、 B、 C、 D、二、多选题
-
15. 函数 的部分图象如图所示,下列结论中正确的是( )
 A、将函数 的图象向右平移 个单位得到函数 的图象 B、函数 的图象关于点 对称 C、函数 的单调递增区间为 D、直线 是函数 图象的一条对称轴16. 已知函数 的最小正周期为 ,则下列判断正确的有( )A、将函数 图像向左平移 个单位得到函数 的图像 B、函数 在区间 单调递减 C、函数 的图像关于点 对称 D、函数 取得最大值时 的取值集合17. 已知函数 (A>0, >0,0< < )的部分图像如图所示,其图像最高点和最低点的横坐标分别为 和 ,图像在y轴上的截距为 .给出下列命题正确的是( )
A、将函数 的图象向右平移 个单位得到函数 的图象 B、函数 的图象关于点 对称 C、函数 的单调递增区间为 D、直线 是函数 图象的一条对称轴16. 已知函数 的最小正周期为 ,则下列判断正确的有( )A、将函数 图像向左平移 个单位得到函数 的图像 B、函数 在区间 单调递减 C、函数 的图像关于点 对称 D、函数 取得最大值时 的取值集合17. 已知函数 (A>0, >0,0< < )的部分图像如图所示,其图像最高点和最低点的横坐标分别为 和 ,图像在y轴上的截距为 .给出下列命题正确的是( ) A、 的最小正周期为2 B、 的最大值为2 C、 D、 为偶函数18. 将函数 的图象上各点横坐标缩短到原来的 (纵坐标不变)得到函数g(x)的图象,则下列说法不正确的是( )A、函数g(x)的图象关于点 对称 B、函数g(x)的周期是 C、函数g(x)在 上单调递增 D、函数g(x)在 上最大值是1
A、 的最小正周期为2 B、 的最大值为2 C、 D、 为偶函数18. 将函数 的图象上各点横坐标缩短到原来的 (纵坐标不变)得到函数g(x)的图象,则下列说法不正确的是( )A、函数g(x)的图象关于点 对称 B、函数g(x)的周期是 C、函数g(x)在 上单调递增 D、函数g(x)在 上最大值是1三、解答题
-
19. 已知函数 ,其中 , , , ,其部分图象如图所示.
 (1)、求函数 的解析式;(2)、已知函数 ,求函数 的单调递增区间.20. 已知函数 = (其中 )的图象与x轴的相邻两个交点之间的距离为 ,且图象上一个最高点为(1)、求 的解析式和单调增区间;(2)、当 ],求 的值域.
(1)、求函数 的解析式;(2)、已知函数 ,求函数 的单调递增区间.20. 已知函数 = (其中 )的图象与x轴的相邻两个交点之间的距离为 ,且图象上一个最高点为(1)、求 的解析式和单调增区间;(2)、当 ],求 的值域.