初中数学浙教版八年级上学期期末复习专题4——逆命题与逆定理、直角三角形
试卷更新日期:2020-12-31 类型:复习试卷
一、单选题
-
1. 下列四组线段中,不能构成直角三角形的是( )A、5,12,13 B、8,15,17 C、3,4,5 D、2,3,42. 下列各组数是勾股数的一组是( )A、7,24,25 B、 C、1.5,2,2.5 D、3. 如右图:三个正方形和一个直角三角形,图形A的面积是( )
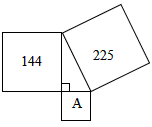 A、225 B、144 C、81 D、无法确定4. 下列定理中没有逆定理的是( )A、等腰三角形的两底角相等 B、平行四边形的对角线互相平分 C、角平分线上的点到角两边的距离相等 D、全等三角形的对应角相等5. 已知一个Rt△的两边长分别为3和4,则第三边长是( )A、5 B、 C、7 D、 或56. 如图,是屋架设计图的一部分,立柱BC垂直于横梁AC , AB=12m , ∠A=30°,则立柱BC的长度为( )
A、225 B、144 C、81 D、无法确定4. 下列定理中没有逆定理的是( )A、等腰三角形的两底角相等 B、平行四边形的对角线互相平分 C、角平分线上的点到角两边的距离相等 D、全等三角形的对应角相等5. 已知一个Rt△的两边长分别为3和4,则第三边长是( )A、5 B、 C、7 D、 或56. 如图,是屋架设计图的一部分,立柱BC垂直于横梁AC , AB=12m , ∠A=30°,则立柱BC的长度为( )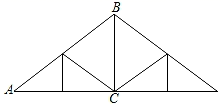 A、4m B、6m C、8m D、12m7. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为5m,梯子的顶端B到地面的距离为12m,现将梯子的底端A向外移动到A',使梯子的底端A'到墙根O的距离等于6m,同时梯子的顶端B下降至B',那么BB'( )
A、4m B、6m C、8m D、12m7. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为5m,梯子的顶端B到地面的距离为12m,现将梯子的底端A向外移动到A',使梯子的底端A'到墙根O的距离等于6m,同时梯子的顶端B下降至B',那么BB'( )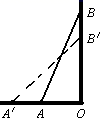 A、小于1m B、大于1m C、等于1m D、小于或等于1m8. 下列命题中,为真命题的是( )A、对顶角相等 B、同位角相等 C、若a2=b2 , 则a=b D、若a>b,则-2a>-2b9. 如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点 出发,沿长方体表面到点 处吃食物,那么它爬行最短路程是( )
A、小于1m B、大于1m C、等于1m D、小于或等于1m8. 下列命题中,为真命题的是( )A、对顶角相等 B、同位角相等 C、若a2=b2 , 则a=b D、若a>b,则-2a>-2b9. 如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点 出发,沿长方体表面到点 处吃食物,那么它爬行最短路程是( ) A、 B、 C、 D、10. 如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1= ;再过点P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2017=( )
A、 B、 C、 D、10. 如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1= ;再过点P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2017=( )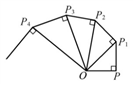 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 命题“若a=b,则﹣a=﹣b”的逆命题是.12. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,若AB=8,则BD= .
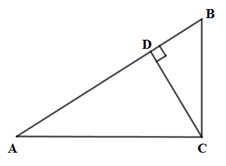 13. 如图Rt△ABC , ∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=3,BC=4时,则阴影部分的面积为 .
13. 如图Rt△ABC , ∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=3,BC=4时,则阴影部分的面积为 .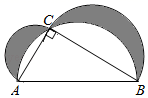 14. 如图,已知△ABD,△BCE均为等腰直角三角形,若CD=8,BE=3,则AC等于 .
14. 如图,已知△ABD,△BCE均为等腰直角三角形,若CD=8,BE=3,则AC等于 .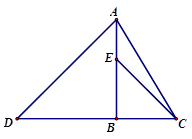 15. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为 ,较短的直角边长为 ,若 ,小正方形的面积为9,则大正方形的边长为.
15. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为 ,较短的直角边长为 ,若 ,小正方形的面积为9,则大正方形的边长为.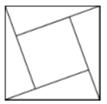
三、综合题
-
16. 如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=
 (1)、求AC、CE的长;(2)、求证:∠ACE=90°.17. 如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,连接AC。
(1)、求AC、CE的长;(2)、求证:∠ACE=90°.17. 如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,连接AC。 (1)、求AC的长度。(2)、求证△ACD是直角三角形。(3)、求四边形ABCD的面积?18. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点.
(1)、求AC的长度。(2)、求证△ACD是直角三角形。(3)、求四边形ABCD的面积?18. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点.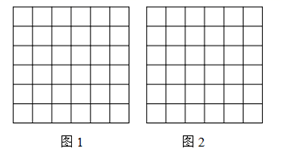 (1)、在图1中以格点为顶点画一条线段MN,使长MN= .(2)、在图2中以格点为顶点画△ABC,使AB= ,AC= ,BC=5.并判断它是否是直角三角形.19. 如图,在△ABC中,AB=AC=4,∠B=∠C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)、在图1中以格点为顶点画一条线段MN,使长MN= .(2)、在图2中以格点为顶点画△ABC,使AB= ,AC= ,BC=5.并判断它是否是直角三角形.19. 如图,在△ABC中,AB=AC=4,∠B=∠C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E. (1)、当∠BDA=120°时,∠EDC;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
(1)、当∠BDA=120°时,∠EDC;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.