初中数学浙教版八年级上学期期末复习专题3——轴对称、等腰三角形
试卷更新日期：2020-12-31 类型：复习试卷
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 如果等腰三角形的一个外角为140°，那么底角为（ ）A、40° B、60° C、70° D、40°或70°3. 已知 是 的两边，且 ，则 的形状是（ ）A、等腰三角形 B、等边三角形 C、锐角三角形 D、不确定4. 如图，正方形网格中的网格线交点称为格点．△ABC的三个顶点为三个格点，如果P是图中异于C点的格点，且以A，B，P为顶点的三角形与△ABC全等，则符合条件的P点有（ ）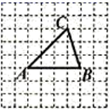
A、1个 B、2个 C、3个 D、4个5. 如图， 中， ， 是 中点，下列结论中错误的是（ ）．
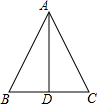A、 B、 C、 平分 D、6. 若一个等腰三角形的两边长分别为 4，5，则这个等腰三角形的周长为（ ）A、13 B、14 C、13 或 14 D、8或 107. 如图，在△ABC中，BF、CF分别平分∠ABC和∠ACB ， 过点F作EG∥BC分别交于点AB、AC于点E、G ． 若AB=9，BC=10，AC=11，则△AEG的周长为（ ）
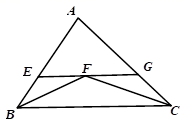A、15 B、20 C、21 D、198. 下列三角形：①有两个角等于60°的三角形；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（ ）A、①②③④ B、①②④ C、①③ D、②③④9. 如图， ， ， ，若 ，则 （ ）
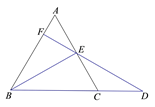A、 B、 C、 D、10. 如图，已知：∠MON=30°，点A1、A2、A3、…在射线ON上，点B1、B2、B3、…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形，若OA1=1，则△A9B9A10的边长为（ ）
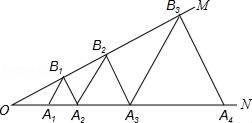A、32 B、64 C、128 D、256二、填空题
-
11. 在△ABC中，已知∠B=∠C，AB=5，则AC的长为 ．12. 若等腰三角形一腰上的高与另一腰的夹角为 ，则这个等腰三角形的顶角的度数为 ．13. 如图，在 的正方形格纸中，有一个以格点为顶点的 ，请你找出格纸中所有与 成轴对称且也以格点为顶点的三角形，这样的三角形共有个.
14. 如图是一个台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔．若一个球按图中所示的方向被击出(球可以经过多反射)，则该球最后将落入的球袋是。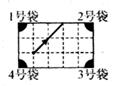
15. 如图，△ABC中，AB＝AC，BC＝4，△ABC的面积为20，腰AC的垂直平分线EF分别交边AC，AB于点E，F，若D为BC边的中点，M为线段EF上一动点，则△CDM的周长的最小值为 ．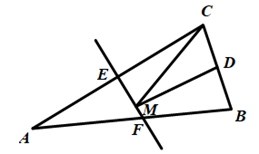
三、综合题
-
16. 已知：如图，点M在锐角∠AOB的内部，在OA边上求作一点P ， 在OB边上求作一点Q ， 使得△PMQ的周长最小．
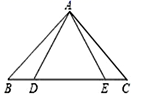
17. 已知：如图， AB=AC，AD=AE．求证：BD=CE．
