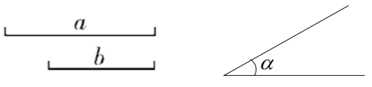初中数学浙教版八年级上学期期末复习专题1——认识三角形、定义与命题、证明
试卷更新日期:2020-12-31 类型:复习试卷
一、单选题
-
1. 如图所示,为估计池塘两岸A , B间的距离,一位同学在池塘一侧选取了一点P , 测得PA=16m , PB=12m , 那么A , B间的距离不可能是( )
 A、15m B、18m C、26m D、30m2. 一个三角形三个内角的度数之比是3:4:5,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 如图,在△ABC中,∠A=70°,直线DE分别与AB,AC交于D,E两点,则∠1+∠2=( )
A、15m B、18m C、26m D、30m2. 一个三角形三个内角的度数之比是3:4:5,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 如图,在△ABC中,∠A=70°,直线DE分别与AB,AC交于D,E两点,则∠1+∠2=( )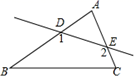 A、110° B、140° C、180° D、250°4. 三角形的重心是三角形的( )A、三条角平分线的交点 B、三条垂直平分线的交点 C、三条高线的交点 D、三条中线的交点5. △ABC中,AB=AC , ∠A=∠C , 则∠B=( )A、36° B、45° C、60° D、90°6. 下列语句中,不是命题的是( )A、作线段AB B、对顶角相等 C、互补的两个角不相等 D、直角都等于90°7. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A、110° B、140° C、180° D、250°4. 三角形的重心是三角形的( )A、三条角平分线的交点 B、三条垂直平分线的交点 C、三条高线的交点 D、三条中线的交点5. △ABC中,AB=AC , ∠A=∠C , 则∠B=( )A、36° B、45° C、60° D、90°6. 下列语句中,不是命题的是( )A、作线段AB B、对顶角相等 C、互补的两个角不相等 D、直角都等于90°7. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )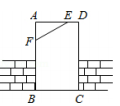 A、两点之间的线段最短 B、两点确定一条直线 C、三角形具有稳定性 D、长方形的四个角都是直角8. 如图, , , ,则 的大小是( )
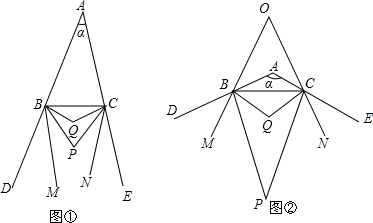
A、两点之间的线段最短 B、两点确定一条直线 C、三角形具有稳定性 D、长方形的四个角都是直角8. 如图, , , ,则 的大小是( ) A、 B、 C、 D、9. 如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
A、 B、 C、 D、9. 如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( ) A、∠DOE的度数不能确定 B、∠AOD= ∠EOC C、∠AOD+∠BOE=60° D、∠BOE=2∠COD10. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( )
A、∠DOE的度数不能确定 B、∠AOD= ∠EOC C、∠AOD+∠BOE=60° D、∠BOE=2∠COD10. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( ) A、19.2° B、8° C、6° D、3°
A、19.2° B、8° C、6° D、3°二、填空题
-
11. 如图,∠B=∠C=30°.∠A=40°,∠ADC的度数为 .
 12. 一个三角形的三个内角中,至少有个锐角.13. 已知三角形的两边长分别是 和 ,则第三边长a的取值范围是 .14. 已知如图,在Rt△ABC中,∠B=90°,AB=BC,AD平分∠BAC,DE⊥AC于E.若AC=10,可求得△DEC的周长为 .
12. 一个三角形的三个内角中,至少有个锐角.13. 已知三角形的两边长分别是 和 ,则第三边长a的取值范围是 .14. 已知如图,在Rt△ABC中,∠B=90°,AB=BC,AD平分∠BAC,DE⊥AC于E.若AC=10,可求得△DEC的周长为 . 15. 有三条两两相交的公路,要建一个加油站,使它到三条公路的距离相等,那么加油站可建的地点有个.
15. 有三条两两相交的公路,要建一个加油站,使它到三条公路的距离相等,那么加油站可建的地点有个. 16. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中 面积相等的是 .
16. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中 面积相等的是 .
三、综合题
-
17. 指出下列命题的条件和结论,并改写成“如果……那么……”的形式:(1)、对顶角相等;(2)、同角的余角相等;(3)、三角形的内角和等于180°;(4)、角平分线上的点到角的两边距离相等.18. 尺规作图,请作出∠AOB的角平分线OC.(不写作图过程,只保留作图迹)
 19. 已知:线段 、 和 ,如图,求作: ,使 , , .(保留作图痕迹,不写作法)
19. 已知:线段 、 和 ,如图,求作: ,使 , , .(保留作图痕迹,不写作法)