浙江省绍兴市柯桥区2021届九年级上学期数学12月月考试卷

试卷更新日期：2020-12-30 类型：月考试卷

进入出卷网下载

一、选择题(本大题共10小题，每小题4分，共40分.)

1. 计算sin²30°+cos²60°的结果为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、1 D、 $\frac{1}{4}$

查看试题解析
2. 如图，直线a，b，c被直线l₁ ， l₂所截，交点分别为点A，C，E和点B，D，F.已知a∥b∥c，且AC＝3，CE＝4，则 $\frac{B D}{B F}$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
3. 抛一个杯口和杯底大小不同的纸杯，落地有三种可能性：①杯口向上②杯底向上③侧面着地，则杯口向上的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、只能用大量重复试验，频率估计概率的方法求得

查看试题解析
4. 把边长相等的正五边形ABCDE和正方形ABFG，按照如图所示的方式叠合在一起，连结AD，则∠DAG＝（）

A、18° B、20° C、28° D、30°

查看试题解析
5. 如图，已知扇形的圆心角为60°，半径为3，则图中弓形（阴影部分）的面积为（）

A、6π﹣9 $\sqrt{3}$ B、6π﹣3 $\sqrt{3}$ C、 $\frac{6 π - 9 \sqrt{3}}{4}$ D、 $\frac{6 π - 9 \sqrt{3}}{2}$

查看试题解析
6. 如图，在4×4的正方形网格中，画2个相似三角形，在下列各图中，正确的画法有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，某大桥可以近似地看作半径为250m的圆中的一段圆弧，桥拱和路面之间用数根钢索垂直相连，其正下方的路面AB长度为300m，那么这些钢索中最长的一根为（）

A、60m B、50m C、45m D、40m

查看试题解析
8. 一块直角三角形木板，它的一条直角边AC长为1cm，面积为1cm² ，甲、乙两人分别按图①、②把它加工成一个正方形桌面，则①、②中正方形的面积较大的是（）

A、① B、② C、一样大 D、无法判断

查看试题解析
9. 已知二次函数y＝ax²+bx+c（a，b，c是常数，a≠0）的y与x的部分对应值如下表：下列结论正确是（）

x

…

-3

-2

-1

0

1

…

y

…

-3

0

1

0

-3

…

①ab＞0 ②a+b+c＜0 ③若点（﹣7，y₁），点（7，y₂）在二次函数图象上，则y₁＜y₂④方程ax²+bx+c＝﹣3有两个不相等的实数根

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
10. 木工师傅要把一根质地均匀的圆柱形木料锯成若干段，按着如图的方式锯开，每锯断一次所用的时间均相同.若锯成n段（n≥2，且n为整数）需要时间是m分，则锯成2n段，需要的时间是（）

A、2m分 B、2（m﹣1）分 C、 $\frac{2 m n}{n - 1}$ 分 D、 $\frac{m (2 n - 1)}{n - 1}$ 分

查看试题解析

二、填空题(本大题共6小题，每小题5分，共30分)

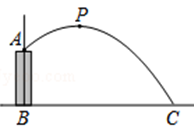
11. 一个不透明的布袋里装有7个只有颜色不同的球，其中4个白球，2个红球，1个黄球，从布袋里任意摸出1个球，是红球的概率是.

查看试题解析
12. 如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2m，喷出水流的运动路线是抛物线，如果水流的最高点P到喷水枪AB所在直线的距离为2m，且到地面的距离为3m，则水流的落地点C到水枪底部B的距离为.

查看试题解析
13. 如图，线段CD两个端点的坐标分别为C（4，4），D（6，2），以原点O为位似中心，在第一象限内将线段CD缩小为原来的一半后得到线段AB，则端点A的坐标为.

查看试题解析
14. 如图，△ABC的顶点都是正方形网格中的格点，则tan∠ACB的值为.

查看试题解析
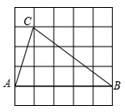15. 相邻两根电杆都用钢索在地面上固定，如图，一根电杆钢索系在离地面4米处，另一根电杆钢索系在离地面6米处，两根电线杆的钢索都有一根固定在另一根电线杆底部，则中间两根钢索相交处点P离地面米

查看试题解析
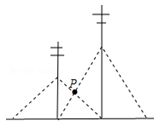16. 如图，AB是圆O的直径，M、N是弧AB（异于A、B）上两点，C是劣弧MN上一动点，∠ACB的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比值是.

查看试题解析

三、解答题(本大题共8小题，共80分。)

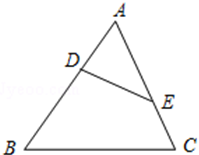
17. 手机微信中的抢红包游戏有一种玩法为“拼手气红包”：用户设定好总金额以及红包个数之后，可以生成金额均不等的红包.现有四个人组成的微信群中，其中一人发了三个“拼手气红包”，其他三人随机抢红包.

(1)、若甲的速度最快，求甲抢到最多金额的红包的概率；

(2)、若三个人同时点击红包，记金额最多、居中、最少的红包分别为A、B、C，试求出甲抢到红包A的概率P_（_A_）.

查看试题解析
18. 如图，D、E分别是△ABC的边AB、AC上的点，AB＝9，BD＝7，AC＝6，CE＝3，求证：△ADE∽△ACB.

查看试题解析
19. 已知二次函数图象的对称轴为y轴，且经过点（1，5）和（﹣ $\frac{1}{2}$ ， $\frac{11}{4}$ ）.

(1)、求此二次函数的解析式；

(2)、若将该二次函数先向下平移4个单位，再沿x轴翻折后与x轴交于A，B两点，设顶点为P，求△AOP的面积.

查看试题解析
20. 已知：如图，∠PAC＝30°，在射线AC上顺次截取AD＝3cm，DB＝10cm，以DB为直径作⊙O交射线AP于E、F两点.

(1)、求圆心O到AP的距离；

(2)、求弦EF的长.

查看试题解析
21. 如图是一种简易台灯的结构图，灯座为△ABC（BC伸出部分不计），A、C、D在同一直线上.量得∠ACB＝90°，∠A＝60°，AB＝16cm，∠ADE＝135°，灯杆CD长为40cm，灯管DE长为15cm.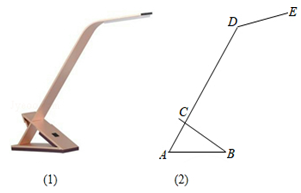

(1)、求DE与水平桌面（AB所在直线）所成的角；

(2)、当E点到水平桌面（AB所在直线）的距离介于45cm至46cm范围时，视线最佳，通过计算说明此时光线是否为最佳.（参考数据：sin15°＝0.26，cos15°＝0.97，tan15°＝0.27， $\sqrt{3}$ ＝1.73.）

查看试题解析
22. 某商店销售一种进价50元/件的商品，经市场调查发现：该商品的每天销售量y（件）是售价x（元/件）的一次函数，其售价、销售量的二组对应值如下表：

售价x（元/件）

55

65

销售量y（件/天）

90

70

(1)、若某天销售利润为800元，求该天的售价为多少元/件.

(2)、由于某种原因，该商品进价提高了a元/件（a＞0），商店售价不低于进价，物价部门规定该商品售价不得超过70元件，该商店在今后的销售中，每天能获得的销售最大利润是960元，求a的值.

查看试题解析
23. 如图，在平面直角坐标系中，有Rt△ABC，∠ACB＝90°，∠BAC＝30°，点A、B均在x轴上，边AC与y轴交于点D，连结BD，点B的坐标为（ $\sqrt{3}$ ，0），若BD是∠ABC的角平分线.

(1)、如图1，求点C的坐标；

(2)、如图2，将Rt△ABC绕点A逆时针旋转一个角度α（0°≤α≤180°）得到Rt△AB'C'，直线AC'交直线BD于点P，直线AB'交y轴于点Q，是否存在点P、Q，使△APQ为等腰三角形？若存在，直接写出∠APQ的度数；若不存在，请说明理由.

查看试题解析
24. 如图，在平面直角坐标系xOy中，已知点A（0，4），点B是x轴正半轴上一点，连结AB，过点A作AC⊥AB，交x轴于点C，点D是点C关于点A的对称点，连结BD，以AD为直径作⊙Q交BD于点E，连结AE并延长交x轴于点F，连结DF.

(1)、求线段AE的长；

(2)、若AB﹣BO＝2，求tan∠AFC的值；

(3)、若△DEF与△AEB相似，求 $\frac{B E}{D E}$ 的值.

查看试题解析

x	…	-3	-2	-1	0	1	…
y	…	-3	0	1	0	-3	…

售价x（元/件）	55	65
销售量y（件/天）	90	70