浙江省绍兴市柯桥区2020-2021学年八年级上学期数学12月月考试卷
试卷更新日期：2020-12-30 类型：月考试卷
一、单选题（共10题；共20分）
-
1. 剪纸艺术是我国文化宝库中的优秀遗产，在民间广泛流传．下面四幅剪纸作品中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 如图所示，在△ABC中，AC = AD = BD，∠DAC = 80°，则∠B的度数是（ ）
A、40 B、35 C、25 D、203. 能说明命题“若x（x+1）（x﹣2）＝0，则x＝0”是假命题的反例是（ ）A、x＝0 B、x＝﹣2 C、x＝1 D、x＝﹣14. 不等式3x+6≥9的解集在数轴上表示正确的是（ ）A、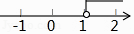
B、
C、
D、
5. 如果点P（m，1﹣m）在第四象限，则m的取值范围是（ ）A、m＞0 B、0＜m＜1 C、m＜1 D、m＞16. 一块三角形玻璃被打碎后，店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃，能够全等的依据是（ ）
A、 B、 C、 D、7. 如果不等式组 的解集是x＞7，则n的取值范围是（ ）A、n=7 B、n＜7 C、n≥7 D、n≤78. 如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于 MN的长为半径画弧，两弧在第二象限交于点P.若点P的坐标为（2x，y+1），则y关于x的函数关系为（ ）
A、y＝x B、y＝﹣2x﹣1 C、y＝2x﹣1 D、y＝1﹣2x9. 某仓库调拨一批物资，调进物资共用8小时，调进物资4小时后同时开始调出物资（调进与调出的速度保持不变）.该仓库库存物资m（吨）与时间t（小时）之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是（ ）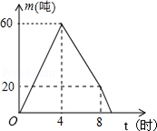
A、8.4小时 B、8.6小时 C、8.8小时 D、9小时10. 如图，直角坐标系中，O为原点，A（12，0），在等腰三角形ABO中，OB＝BA＝10，点B在第一象限，C为y轴正半轴上一动点，作以∠CBD为顶角的等腰三角形CBD，且∠CBD＝∠OBA，连接AD并延长与y轴交于点M（0，m），则m的值为（ ）.
A、 B、 C、 D、二、填空题（共10题；共30分）
-
11. 函数y= 中，自变量x的取值范围为 ．12. 已知y=kx的正比例函数，当x＝﹣2时，y＝4，则k＝.13. 已知点A的坐标为（﹣2，3），则点A关于x轴的对称点的坐标是14. 不等式 的负整数解为.15. 命题“等腰三角形两腰上的高相等”的逆命题是.16. 如图，两个一次函数图象的交点坐标为（2，4），则关于x，y的方程组 的解为.
17. 定义：△ABC中，一个内角的度数为α，另一个内角的度数为β，若满足α+2β＝90°，则称这个三角形为“智汇三角形”.在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，D是BC上的一个动点，连接AD，若△ABD是“智汇三角形”，则CD的长是18. 在如图所示的三个函数图象中，近似地刻画如下a、b、c三个情境：
情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；
情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进.
情境c：小芳从家出发，到学校上学，放学回到了家.
情境a，b，c所对应的函数图象分别是（按次序填写a，b，c对应的序号）
19. 如图，四边形ABCD是长方形，AB=x，BC=4，点P为直线AD上的一点.若满足△BCP为等腰三角形的点P有且仅有3个，则x需满足的条件是.
20. 如图，平面直角坐标系中，已知点P（2，2），C为y轴正半轴上一点，连接PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线OP交于点A，且BD＝4AD，直线CD与直线OP交于点Q，则点Q的坐标为.
三、解答题(本大题共7小题，共50分。)
-
21. 解不等式组解不等式组： ，并与出它的整数解..22. 如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）
(1)、写出点A、B的坐标：A（）、B（）
(2)、判断△ABC的形状.计算△ABC的面积是.(3)、将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，若△ABC内一点p的坐标是（a，b），则点P在△A′B′C′内的对应点P′的坐标是 。23. 如图，AC与BD相交于点E，AC＝BD，AC⊥BC，BD⊥AD.垂足分别是C、D.
(1)、求证：△ADB≌△BCA；(2)、若AC＝6，且∠BAC=30°，求AD的长.24. 随着“新年”临近，儿童礼品开始热销，某厂每月固定生产甲、乙两种礼品共100万件，甲礼品每件成本15元，乙礼品每件成本12元，现甲礼品每件售价22元，乙礼品每件售价18元，且都能全部售出．(1)、若某月甲礼品的产量为x万件，总利润为y万元，写出y关于x的函数关系式．(2)、如果每月投入的总成本不超过1380万元，应怎样安排甲、乙礼品的产量，可使所获得的利润最大？25. 阅读下面材料：
【原题呈现】如图1，在△ABC中，∠A=2∠B，CD平分∠ACB，AD=2.2，AC=3.6，求BC的长.
【思考引导】因为CD平分∠ACB，所以可在BC边上取点E，使EC=AC，连接DE.这样很容易得到△DEC≌△DAC，经过推理能使问题得到解决（如图2）.
【问题解答】
(1)、参考提示的方法，解答原题呈现中的问题：(2)、拓展提升：如图3，已知△ABC中，AB=AC，∠A=20°，BD平分∠ABC，BD=2.3，BC=2.求AD的长.
26. 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x(h)，两车之间的距离为y，图中的折线表示y与x之间的函数关系.
(1)、①甲、乙两地之间的距离为千米；②释图中点B的实际意义：
(2)、求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；(3)、若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同.在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时？
27. 如图，直线y＝﹣x﹣6交x轴和y轴于点A和点C，点B（0，3）在y轴上，连接AB，点P为直线AB上一动点.
(1)、直线AB的解析式为；(2)、若S△APC＝S△AOC ， 求点P的坐标；(3)、当∠BCP＝∠BAO时，求直线CP的解析式.(4)、附加分3分，计入总分，得分不超过100分：若点P为线段AC（不含端点）上一动点，将线段OP绕点O逆时针旋转90°，得线段OQ，连接BQ，△OBQ周长的最小值为.