浙江省宁波市慈溪市2021届九年级上学期数学12月月考试卷

试卷更新日期：2020-12-30 类型：月考试卷

进入出卷网下载

一、选择题(每小题4分，共40分.)

1. 下列关系式中，属于二次函数的是（）

A、 $y = 3 x^{2} - 2 x - 1$ B、 $y = - 4 x$ C、 $y = x + 5$ D、 $y = \frac{- 1}{x}$

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、某校九年级共有428人，至少有两人的生日一样 B、经过路口，恰好遇到绿灯 C、打开电视，正在播放广告 D、抛一枚硬币，正面朝上

查看试题解析
3. 若 $\frac{y}{x}$ = $\frac{3}{4}$ ，则 $\frac{x + y}{x}$ 的值为（）

A、3 B、 $\frac{4}{7}$ C、 $\frac{7}{3}$ D、 $\frac{7}{4}$

查看试题解析
4. 下列四个命题中，正确的有（）

A、圆的对称轴是直径 B、半径相等的两个半圆是等弧 C、三角形的外心到三角形各边的距离相等 D、经过三个点一定可以作圆

查看试题解析
5. 抛物线y=-2(x+3)²的顶点在（）

A、x轴正半轴上 B、x轴负半轴上 C、y轴正半轴上 D、y轴负半轴上

查看试题解析
6. 若∠A为锐角，且cosA<0.5，则∠A（）

A、小于30° B、大于30° C、大于60° D、大于60°

查看试题解析
7. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15米，如图所示，然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（）

A、10米 B、12米 C、15米 D、22.5米

查看试题解析
8. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则下列结论中正确的是（）

A、a>0 B、b>0 C、c>0 D、b²-4ac>0

查看试题解析
9. 在Rt△ABC中，∠C=90°，若sinA= $\frac{2}{3}$ ，则tanB=（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
10. 已知正方形MNOK和正六边形ABCDEF的边长均为1，把正方形放在正六边形中，使OK边与AB边重合，如图所示，按下列步骤操作：将正方形在正六边形中绕点B顺时针旋转，使KM边与BC边重合，完成第一次旋转；再绕点C顺时针旋转，使MN边与CD边重合，完成第二次旋转，……，在这样连续6次旋转的过程中，点B，M之间的距离可能是（）

A、1.4 B、1.1 C、0.8 D、0.5

查看试题解析

二、填空题(每小题5分，共30分)

11. 已知⊙O的半径是5，点P不在⊙O外，则线段OP的长得取值范围是.

查看试题解析
12. 计算：sin60°+cos30°=.

查看试题解析
13. 如图所示，点A，B，C是⊙O上三点，∠AOB=110°，则∠ACB=°.

查看试题解析
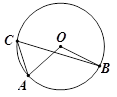14. 学校团委在“五四”青年节举行“感动校园十大人物”颁奖活动，九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动，则甲、乙两人中恰好有一人参加此活动的概率是.

查看试题解析
15. 将进货单价为70元的某种商品按零售单价100元售出时，每天能卖出40个，若这种商品的零售单价在一定范围内每降价1元，其日销量就增加2个，为了获取最大的日利润，则应把零售单价定为元.

查看试题解析
16. 如图，⊙O是△ABC的外接圆，已知AD平分∠BAC交⊙O于点D，交BC于点E，若BD=6，AE=5，AB=7，则AC=.

查看试题解析

三、解答题(17~19题各8分，20~22题各10分，23题12分，24题14分，共80分)

17. 如图，已知AB∥CD，AD、BC 交于点E.

(1)、写出所有比值等于 $\frac{A E}{B E}$ 的两条线段之比.

(2)、若AE=3，DE=6，BC=12，求CE的长.

查看试题解析
18. 已知抛物线y =x²+bx-1经过(3，-4).

(1)、求抛物线的解析式.

(2)、求抛物线的对称轴，并指出当x取何值时，y随着x的增大而减小.

查看试题解析
19. 如图，矩形ABCD中，AB =6，BC=3，以点A为圆心，AB为半径的弧交CD于点E.

(1)、求∠AED的度数.

(2)、求扇形ABE的面积.

查看试题解析
20. 小覃和小莫两位同学在学习“概率”时，做投掷骰子(质地均匀的正方体)实验，他们共做了100次试验，实验的结果如下：

向上点数

1

2

3

4

5

6

出现次数

12

19

15

18

20

x

(1)、求表格中x的值.

(2)、计算“3点朝上”的频率.

(3)、小覃说：“根据实验，一次实验中出现1点朝上的概率是12%”；小覃的这一说法正确吗?为什么?

(4)、小莫说：“如果掷6000次，那么出现5点朝上的次数大概是1500次左右.”小莫的这一说法正确吗?为什么?

查看试题解析
21. 据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过50km/h.如图，在一条笔直公路l的旁边A处有一探测仪，AD⊥l于D，AD=32m，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=28°，2秒后到达C点，测得∠ACD=45°.(sin28°≈ 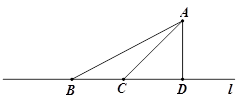$\frac{8}{17}$ ，cos28°≈ $\frac{15}{17}$ ，tan28°≈ $\frac{8}{15}$ )

(1)、求CD，BD的长度.

(2)、通过计算，判断此轿车是否超速.

查看试题解析
22. 如图，在▱ABCD中，AE：EB=3：2，DE交AC于点F.

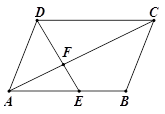(1)、求证：△AEF∽△CDF.

(2)、求△CDF与△AEF周长之比.

(3)、如果△CDF的面积为50cm² ，直接写出四边形BCFE的面积.

查看试题解析
23. 如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交AC于点E.

(1)、求证：BD=CD.

(2)、若 $\overset{⌢}{D E}$ =54°，求∠AED的度数.

(3)、过点D作DF⊥AB于点F，若BC=12，AF=3BF， $\overset{⌢}{B D}$ 的长.

查看试题解析
24. 如图，在矩形OABC中，点O为原点，点A的坐标为(0，8)，点C的坐标为(6，0).抛物线y= $- \frac{4}{9}$ x²+bx+c经过点A、C，与AB交于点D.点P为线段BC上一个动点(不与点C重合)，点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S.

(1)、求抛物线的函数解析式.

(2)、求S关于m的函数表达式.

(3)、当S最大时，①求点Q的坐标.②若点F在抛物线y= $- \frac{4}{9}$ x²+bx+c的对称轴上，且△DFQ的外心在DQ上，求点F的坐标.

查看试题解析

向上点数	1	2	3	4	5	6
出现次数	12	19	15	18	20	x