浙江省宁波市慈溪市2020-2021学年八年级上学期数学12月月考试卷
试卷更新日期:2020-12-30 类型:月考试卷
一、选择题(共30分,每小题3分)
-
1. 环保理念深入人心,垃圾分类的标识中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,下列各点在第二象限的是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)3. 不等式x﹣1>0 的解在数轴上表示为( )
2. 在平面直角坐标系中,下列各点在第二象限的是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)3. 不等式x﹣1>0 的解在数轴上表示为( )
A、 B、
B、 C、
C、 D、
D、 4. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
4. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( ) A、AB=ED B、AC=DF C、BF=EC D、∠A=∠D5. 已知三角形三边为a,b,c,其中a=3cm,b=4cm,线段c不能取( )A、2cm B、4cm C、6cm; D、8cm6. 命题“若a2=b2 , 则a=b”。能说明这个命题是假命题的是( )A、a=3,b=3 B、a=﹣3,b=﹣3 C、a=3,b=﹣3 D、a=﹣3,b=﹣27. 若x+a<y+a,ax>ay,则( )
A、AB=ED B、AC=DF C、BF=EC D、∠A=∠D5. 已知三角形三边为a,b,c,其中a=3cm,b=4cm,线段c不能取( )A、2cm B、4cm C、6cm; D、8cm6. 命题“若a2=b2 , 则a=b”。能说明这个命题是假命题的是( )A、a=3,b=3 B、a=﹣3,b=﹣3 C、a=3,b=﹣3 D、a=﹣3,b=﹣27. 若x+a<y+a,ax>ay,则( )
A、x>y,a>0 B、x>y,a<0 C、x<y,a>0 D、x<y,a<08. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、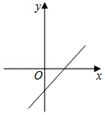 B、
B、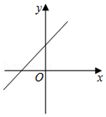 C、
C、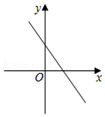 D、
D、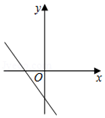 9. 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
9. 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( ) A、4 B、6 C、8 D、1010. 如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是( )
A、4 B、6 C、8 D、1010. 如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是( )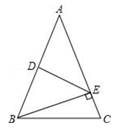 A、6 B、 C、 D、10
A、6 B、 C、 D、10二、填空题(共24分,每小题4分)
-
11. "对顶角相等"的逆命题是 。12. 函数 中,自变量x的取值范围是 .13. 在平面直角坐标系中,已知一次函数y=﹣ x+1的图象经过P1(x1 , y1),P2(x2 , y2)两点,若x1>x2 , 则y1y2.14. 如图,已知O为△ABC三边垂直平分线的交点,∠A=50°,则∠BOC的度数为度。
 15. 如图,已知A(2,2)、B(﹣4,1),点P在y轴上,则当y轴平分∠APB时,点P的坐标为.
15. 如图,已知A(2,2)、B(﹣4,1),点P在y轴上,则当y轴平分∠APB时,点P的坐标为.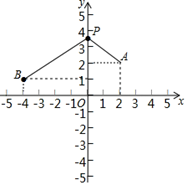 16. 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1 , l2 , l3 , ……ln分别变于点A1 , A2 , A3 , ……An;函数y=3x的图象与直线l1 , l2 , l3 , ……ln分别交于点B1 , B2 , B3 , ……Bn , 如果△OA1B1的面积记的作S1 , 四边形A1A2B2B1的面积记作S2 , 四边形A2A3B3B2的面积记作S3 , …四边形An﹣1AnBnBn﹣1的面积记作Sn , 那么S2020=.
16. 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1 , l2 , l3 , ……ln分别变于点A1 , A2 , A3 , ……An;函数y=3x的图象与直线l1 , l2 , l3 , ……ln分别交于点B1 , B2 , B3 , ……Bn , 如果△OA1B1的面积记的作S1 , 四边形A1A2B2B1的面积记作S2 , 四边形A2A3B3B2的面积记作S3 , …四边形An﹣1AnBnBn﹣1的面积记作Sn , 那么S2020=.
三、解答题(共66分)
-
17. 解不等式组18. 如图,正方形网格由边长为1的小正方形组成,△ABC的顶点都在格点上,平面直角坐标系的坐标轴落在网格线上,按要求完成作图:

( 1 )作出△ABC关于y轴对称的图形△A1B1C1 , 其中点A1的坐标为▲;
( 2 )在x轴上画出一点Q,使得△ACQ的周长最小.
19. 如图,△BCE,△ACD分别是以BE,AD为斜边的直角三角形,BE=AD,△CDE是等边三角形. (1)、求证:△BCE≌△ACD;(2)、BE与AC垂直吗?若AD=6,求BF的长为.20. 直角坐标系中,直线l1过A(1,3),B(﹣5,﹣3),直线l2经过点(1,-6),且与直线l1交于点(-2,a)。
(1)、求证:△BCE≌△ACD;(2)、BE与AC垂直吗?若AD=6,求BF的长为.20. 直角坐标系中,直线l1过A(1,3),B(﹣5,﹣3),直线l2经过点(1,-6),且与直线l1交于点(-2,a)。 (1)、求直线l1和l2函数表达式;(2)、设直线l2与y轴交于点C,求△ABC的面积。(3)、x轴上存在点P,使△POA成为等腰三角形,直接写出点P的坐标21. 现计划把一批货物用一列火车运往某地.已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.(1)、设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并写出自变量x的取值范围;(2)、已知A型车厢数不少于B型车厢数,估计运输总费用不低于276000元,问符合条件的运送方案中哪种方案运费最低?22. 在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.
(1)、求直线l1和l2函数表达式;(2)、设直线l2与y轴交于点C,求△ABC的面积。(3)、x轴上存在点P,使△POA成为等腰三角形,直接写出点P的坐标21. 现计划把一批货物用一列火车运往某地.已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.(1)、设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并写出自变量x的取值范围;(2)、已知A型车厢数不少于B型车厢数,估计运输总费用不低于276000元,问符合条件的运送方案中哪种方案运费最低?22. 在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处. (1)、如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为°.(2)、如图2,若点F落在边BC上,且AB=CD=6,AD=BC=10,求CE的长.(3)、如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=CD=6,
(1)、如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为°.(2)、如图2,若点F落在边BC上,且AB=CD=6,AD=BC=10,求CE的长.(3)、如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=CD=6,AD=BC=10,求CG的长.
23. 如图①所示,甲、乙两车从A地出发,沿相同路线前往同一目的地,途中经过B地.甲车先出发,当甲车到达B地时,乙车开始出发.当乙车到达B地时,甲车与B地相距 km设甲、乙两车与B地之间的距离分别为y1(km),y2(km),乙车行驶的时间为x(h),y1 , y2与x的函数关系如图②所示. (1)、A,B两地之间的距离为km;(2)、甲车的速度为km/h,乙车的速度为km/h;(3)、当x为何值时,甲、乙两车相距5km?24. 如图1,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等腰直角三角形(∠ACP=90°,点A、C、P按逆时针方向排列);当点C移动到点O时,得到等腰直角三角形AOB(此时点P与点B重合).
(1)、A,B两地之间的距离为km;(2)、甲车的速度为km/h,乙车的速度为km/h;(3)、当x为何值时,甲、乙两车相距5km?24. 如图1,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等腰直角三角形(∠ACP=90°,点A、C、P按逆时针方向排列);当点C移动到点O时,得到等腰直角三角形AOB(此时点P与点B重合).
【初步探究】
(1)、写出点B的坐标;(2)、点C在x轴上移动过程中,作PD⊥x轴,垂足为点D,都有△AOC≌△CDP,请在图2中画出当等腰直角△ACP的顶点P在第四象限时的图形,并求证:△AOC≌△CDP.(3)、【深入探究】当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论,并求出这个图形所对应的函数表达式;(4)、直接写出AP2的最小值为.