天津市东丽区2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、单选题
-
1. 下列长度的三条线段能构成三角形的是( )A、2cm,3cm,5cm B、5cm,6cm,11cm C、3cm,4cm,8cm D、5cm,6cm,10cm2. 在 中,若 , ,则 的度数为( )A、65° B、70° C、75° D、80°3. 在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志,在下列这些示意图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知点 的坐标是 ,则点 关于 轴的对称点的坐标是( )A、 B、 C、 D、5. 已知一个多边形的内角和等于900º,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形6. 如图, ,点 和点 ,点 和点 是对应点,如果 , , ,那么 的长是( )
4. 已知点 的坐标是 ,则点 关于 轴的对称点的坐标是( )A、 B、 C、 D、5. 已知一个多边形的内角和等于900º,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形6. 如图, ,点 和点 ,点 和点 是对应点,如果 , , ,那么 的长是( ) A、5cm B、6cm C、7cm D、8cm7. 下列说法正确的个数有( )
A、5cm B、6cm C、7cm D、8cm7. 下列说法正确的个数有( )①三角形的高、中线、角平分线都是线段;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A、1个 B、2个 C、3个 D、4个8. 如图, 中, ,沿 折叠 ,使点 恰好落在 边上的点 处,若 ,则 等于( ) A、59° B、66° C、68° D、69°9. 若一个三角形的三个内角度数的比为 ,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形10. 如图, 关于直线 进行轴对称变换后得到 ,下列说法中错误的是( )
A、59° B、66° C、68° D、69°9. 若一个三角形的三个内角度数的比为 ,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形10. 如图, 关于直线 进行轴对称变换后得到 ,下列说法中错误的是( ) A、 B、直线 垂直平分 、 C、 D、 ,11. 如图, , ,垂足分别为点 ,点 , 、 相交于点O , ,则图中全等三角形共有( )
A、 B、直线 垂直平分 、 C、 D、 ,11. 如图, , ,垂足分别为点 ,点 , 、 相交于点O , ,则图中全等三角形共有( ) A、2对 B、3对 C、4对 D、5对12. 如图, 和 是 分别沿着 、 边翻折 形成的,若 ,则 的度数为( )
A、2对 B、3对 C、4对 D、5对12. 如图, 和 是 分别沿着 、 边翻折 形成的,若 ,则 的度数为( ) A、100° B、90° C、85° D、80°
A、100° B、90° C、85° D、80°二、填空题
-
13. 如图,四边形ABCD中,AB⊥BC,∠A=∠C=100°,则∠D的度数为度.
 14. 五边形的外角和是 .15. 若点 与点 关于 轴对称,则 .16. 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADB的度数为度.
14. 五边形的外角和是 .15. 若点 与点 关于 轴对称,则 .16. 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADB的度数为度. 17. 如图,三角形纸片中, , , ,沿过点 的直线折叠这个三角形,使点 落在 边的点 处,折痕为 ,则 的周长为 .
17. 如图,三角形纸片中, , , ,沿过点 的直线折叠这个三角形,使点 落在 边的点 处,折痕为 ,则 的周长为 .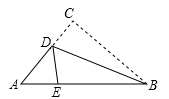 18. 如图,已知 的周长是18, 、 分别平分 和 , 于 ,且 , 的面积是 .
18. 如图,已知 的周长是18, 、 分别平分 和 , 于 ,且 , 的面积是 .
三、解答题
-
19. 如图,已知 , , ,求 的度数.
 20. 一个多边形的内角和比它的外角和的4倍少 ,这个多边形的边数是多少?21. 在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1).
20. 一个多边形的内角和比它的外角和的4倍少 ,这个多边形的边数是多少?21. 在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1). (1)、在图中作出△ABC关于y轴的对称△A1B1C1 .(2)、写出△ABC关于x轴对称△A2B2C2的各顶点坐标.
(1)、在图中作出△ABC关于y轴的对称△A1B1C1 .(2)、写出△ABC关于x轴对称△A2B2C2的各顶点坐标.A2 B2 C2
22. 如图, , , , . (1)、求 的度数;(2)、若 ,求证:
(1)、求 的度数;(2)、若 ,求证:


