河北省石家庄市正定县2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、单选题
-
1. 规定:(→2)表示向右移动2记作+2,则(←3)表示向左移动3记作( )A、+3 B、﹣3 C、﹣ D、+2. 下列运算结果为正数的是( )A、(﹣3)2 B、﹣3÷2 C、0×(﹣2017) D、2﹣33. 有理数 的倒数为( )A、5 B、 C、 D、-54. 如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
 A、60° B、90° C、120° D、150°5. 下列说法正确的是( )A、画直线 B、延长线段 至点 ,使 C、连接两点的线段,就是两点之间的距离 D、如果线段 ,那么点 一定是线段 的中点6. 如图,把 绕点 顺时针旋转 ,得到 , 交 于点 ,若 ,则 度数为( )
A、60° B、90° C、120° D、150°5. 下列说法正确的是( )A、画直线 B、延长线段 至点 ,使 C、连接两点的线段,就是两点之间的距离 D、如果线段 ,那么点 一定是线段 的中点6. 如图,把 绕点 顺时针旋转 ,得到 , 交 于点 ,若 ,则 度数为( )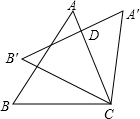 A、45° B、30° C、35° D、70°7. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )A、1cm B、9cm C、1cm或9cm D、以上答案都不对8. 下列说法中,错误的是( )A、零没有相反数. B、最大的负整数是-1. C、互为相反数的两个数到原点的距离相等 D、没有最小的有理数.9. 定义新运算:a⊕b=ab﹣a,例如:3⊕2=3×2﹣3=3,则(﹣3)⊕4=( )A、﹣9 B、12 C、﹣15 D、410. 按如图所示的程序运算:当输入的数据为1时,则输出的数据是( )
A、45° B、30° C、35° D、70°7. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )A、1cm B、9cm C、1cm或9cm D、以上答案都不对8. 下列说法中,错误的是( )A、零没有相反数. B、最大的负整数是-1. C、互为相反数的两个数到原点的距离相等 D、没有最小的有理数.9. 定义新运算:a⊕b=ab﹣a,例如:3⊕2=3×2﹣3=3,则(﹣3)⊕4=( )A、﹣9 B、12 C、﹣15 D、410. 按如图所示的程序运算:当输入的数据为1时,则输出的数据是( )
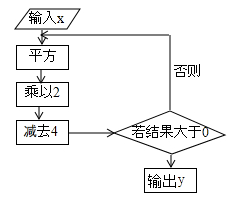 A、2 B、4 C、6 D、811. 如果锐角 的补角是138°,那么锐角 的余角是( )A、38° B、42° C、48° D、52°12. 如图,将方格纸中的图形绕点 逆时针旋转 后得到的图形是( )
A、2 B、4 C、6 D、811. 如果锐角 的补角是138°,那么锐角 的余角是( )A、38° B、42° C、48° D、52°12. 如图,将方格纸中的图形绕点 逆时针旋转 后得到的图形是( )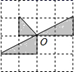 A、
A、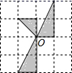 B、
B、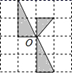 C、
C、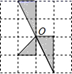 D、
D、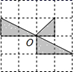 13. 如图,数轴上的 , , 三点所表示的数是分别是 、 、 ,其中 ,如果 ,那么该数轴的原点 的位置应该在( )
13. 如图,数轴上的 , , 三点所表示的数是分别是 、 、 ,其中 ,如果 ,那么该数轴的原点 的位置应该在( )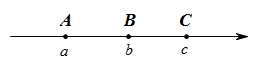 A、点 的左边 B、点 与点 之间 C、点 与点 之间 D、点 与点 之间(靠近点 )或点 的右边14. 为求1+2+22+23+…+22015的值,可令S=1+2+22+23+…+22015 , 则2S=2+22+23+…+22016 , 因此2S﹣S=22016﹣1.仿照以上推理,计算出1+5+52+53+…+52015的值为( )A、52015﹣1 B、52016﹣1 C、 D、
A、点 的左边 B、点 与点 之间 C、点 与点 之间 D、点 与点 之间(靠近点 )或点 的右边14. 为求1+2+22+23+…+22015的值,可令S=1+2+22+23+…+22015 , 则2S=2+22+23+…+22016 , 因此2S﹣S=22016﹣1.仿照以上推理,计算出1+5+52+53+…+52015的值为( )A、52015﹣1 B、52016﹣1 C、 D、二、填空题
-
15. 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
 16. 已知 ,则 =.17. 往返于甲、乙两地的列车,中途需要停靠 个车站,如果每两站的路程都不相同,问:(1)、这两地之间有种不同的票价;(2)、要准备种不同的车票.
16. 已知 ,则 =.17. 往返于甲、乙两地的列车,中途需要停靠 个车站,如果每两站的路程都不相同,问:(1)、这两地之间有种不同的票价;(2)、要准备种不同的车票.三、解答题
-
18. 操作探究:已知在纸面上有一数轴(如图所示).
 (1)、操作一:
(1)、操作一:折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与表示的点重合;
(2)、操作二:折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
19. 计算(1)、(2)、(3)、(4)、20. 若a,b互为相反数,c,d互为倒数,m的绝对值是1,求 的值 .21. 作图题:已知平面上点A,B,C,D.按下列要求画出图形: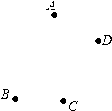
⑴作直线AB,射线CB;
⑵取线段AB的中点E,连接DE并延长与射线CB交于点O;
⑶连接AD并延长至点F,使得AD=DF.
22. 如图所示,已知点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.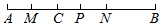 (1)、若AB=12 cm,则MN的长度是cm;(2)、若AC=3 cm,CP=1 cm,求线段PN的长度.23. 某自行车厂计划一周生产自行车 1400 辆,平均每天生产 200 辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产积为负):
(1)、若AB=12 cm,则MN的长度是cm;(2)、若AC=3 cm,CP=1 cm,求线段PN的长度.23. 某自行车厂计划一周生产自行车 1400 辆,平均每天生产 200 辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产积为负):星期
一
二
三
四
五
六
日
增减产值
(1)、根据记录的数据可知该厂本周实际生产自行车多少辆?(2)、该厂实际每日计划计件工资制,每生产一辆车可得 60 元,若超额完成任务,则超过部分每辆另奖 15 元,那么该厂工人这一周的工资总额是多少元?24. 如图,以 的点 为端点画一条射线 , , 分别是 和 的角平分线.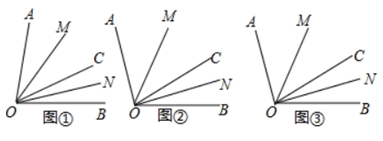 (1)、如图①,若 , ,则 的度数是;(2)、如图②,若 , ,则 的度数是;(3)、根据以上解答过程,完成下列探究:
(1)、如图①,若 , ,则 的度数是;(2)、如图②,若 , ,则 的度数是;(3)、根据以上解答过程,完成下列探究:如图③,当射线OC位于 内部时,请写出 与 的数量关系,并证明你的结论.