河北省石家庄市晋州市2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. 2020的相反数是（）

A、 $\frac{1}{2020}$ B、 $- \frac{1}{2020}$ C、-2020 D、2020

查看试题解析
2. 如果河的水位升高 $0.8 m$ 时水位变化记作 $+ 0.8 m$ ，那么水位下降 $0.5 m$ 时水位变化记作（）

A、 $0.8 m$ B、 $0.5 m$ C、 $- 0.8 m$ D、 $- 0.5 m$

查看试题解析
3. 在﹣ $\frac{1}{2}$ ，0，﹣2， $\frac{1}{3}$ ，1这五个数中，最小的数为（）

A、0 B、﹣ $\frac{1}{2}$ C、﹣2 D、 $\frac{1}{3}$

查看试题解析
4. 如图所示的表面展开图所对应的几何体是（）

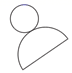A、长方体 B、球 C、圆柱 D、圆锥

查看试题解析
5. 下列说法中，正确的个数有（）
⑴射线AB和射线BA是同一条射线（2）延长射线MN到C（3）延长线段MN到A使NA=2MN（4）连接两点的线段叫做两点间的距离

A、1 B、2 C、3 D、4

查看试题解析
6. 计算 $| - \frac{1}{3} | - \frac{2}{3}$ 的结果是（）

A、 $\frac{1}{3}$ B、-1 C、 $- \frac{1}{3}$ D、1

查看试题解析
7. 下列说法中，正确的个数有（）
①－3.14既是负数，又是小数，也是有理数；②－25既是负数，又是整数，但不是自然数；③0既不是正数也不是负数，但是整数；④0是非负数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如果 $a$ 、 $b$ 两个数在数轴上的位置如图所示，则下列各式正确的是（）

A、 $a + b > 0$ B、 $a b < 0$ C、 $b - a < 0$ D、 $\frac{a}{b} > 0$

查看试题解析
9. 如果a＋b $<$ 0，并且ab $>$ 0，那么（）

A、a $<$ 0，b $<$ 0 B、a $>$ 0，b $>$ 0 C、a $<$ 0，b $>$ 0 D、a $>$ 0，b $<$ 0

查看试题解析
10. 如图，∠AOC＝∠DOE＝90°，如果∠AOE＝65°，那么∠COD的度数是（）

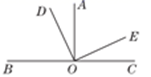A、90° B、115° C、120° D、135°

查看试题解析
11. 若a＝2，|b|＝5，则a＋b＝（）

A、－3 B、7 C、－7 D、－3或7

查看试题解析
12. 下列各组数中，相等的一组是（）

A、 ${(- 3)}^{2}$ 与 $- 3^{2}$ B、 ${| - 3 |}^{2}$ 与 $- 3^{2}$ C、 ${(- 3)}^{3}$ 与 $- 3^{3}$ D、 ${| - 3 |}^{3}$ 与 $- 3^{3}$

查看试题解析
13. 在时刻8：30，时钟上的时针和分针之间的夹角为（）

A、85° B、75° C、70° D、60°

查看试题解析
14. 若 $a > 1$ ，则 $| a |$ ， $- a$ ， $\frac{1}{a}$ 的大小关系正确的是（）

A、 $| a | > - a > \frac{1}{a}$ B、 $\frac{1}{a} > - a > | a |$ C、 $| a | > \frac{1}{a} > - a$ D、 $- a > | a | > \frac{1}{a}$

查看试题解析
15. 如图，数轴上的 $A 、 B 、 C$ 三点所表示的数分别为 $a 、 b 、 c$ ，其中 $A B = B C$ ，如果 $|$ $a | > | c | > | b | ，$ 那么该数轴的原点 $O$ 的位置应该在（）

A、点 $A$ 的左边 B、点 $A$ 与点 $B$ 之间 C、点 $B$ 与点 $C$ 之间 D、点 $C$ 的右边

查看试题解析
16. 若ab≠0，则 $\frac{a}{|a|} + \frac{|b|}{b}$ 的取值不可能是（）

A、0 B、1 C、2 D、－2

查看试题解析

二、填空题

17. 计算|3.14-π|-π的结果是

查看试题解析
18. 如图，点 $C$ 是 $A B$ 的中点， $D$ ， $E$ 分别是线段 $A C$ ， $C B$ 上的点，且 $A D = \frac{2}{3} A C$ ， $D E = \frac{3}{5} A B$ ，若 $A B = 24 c m$ ，则线段 $C E$ 的长为．

查看试题解析
19. 如果规定符号“ $\otimes$ ”的意义是 $a \otimes b = \frac{a b}{a - b}$ ，则 $2 \otimes (- \frac{1}{2})$ 的值是．

查看试题解析

三、解答题

20.

(1)、计算： ${(- 2)}^{2} - | - 6 | + 2 - 3 \times (- \frac{1}{3})$

(2)、计算： ${(- 3)}^{2} - {(1 \frac{1}{2})}^{3} \times \frac{2}{9} - 6 \div | - \frac{2}{3} |$

(3)、已知： $∠ β = 41 ° 3 1^{'}$ ，求： $∠ β$ 的余角的度数．

查看试题解析
21. 把下列各数分类：
$- 8$ ， $0.275$ ， $\frac{22}{7}$ ， $0$ ， $- 1.04$ ， $- (- 3)$ ， $- \frac{1}{3}$ ， $| - 2 |$ ．

正数{   }；

负整数{   }；

分数{   }；

负数{   }．

查看试题解析
22. 阅读理解：
数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如图，线段AB＝1＝0﹣（﹣1）；线段 BC＝2＝2﹣0；线段 AC＝3＝2﹣（﹣1）问题

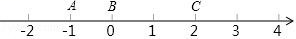(1)、数轴上点M、N代表的数分别为﹣9和1，则线段MN＝；

(2)、数轴上点E、F代表的数分别为﹣6和﹣3，则线段EF＝；

(3)、数轴上的两个点之间的距离为5，其中一个点表示的数为2，则另一个点表示的数为m，求m.

查看试题解析
23. 某足球守门员练习折返跑，从守门员位置出发，向前跑记为正数，向后跑记为负数，他的练习记录如下（单位：米）：

+5

﹣3

+10

﹣8

﹣6

+13

﹣10

(1)、守门员最后是否回到了守门员位置？

(2)、守门员离开守门员位置最远是多少米？

(3)、守门员离开守门员位置达到10米以上（包括10米）的次数是多少？

查看试题解析
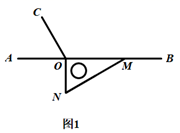
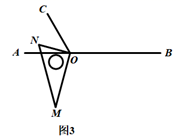24. 如图1， $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，使 $∠ A O C ： ∠ B O C = 1 ： 2$ ．将一直角三角尺的直角顶点放在点 $O$ 处，一边 $O M$ 在射线 $O B$ 上，另一边 $O N$ 在直线 $A B$ 的下方．

(1)、将图1中的三角尺绕点 $O$ 按逆时针方向旋转至图2的位置，使得 $O N$ 落在射线 $O B$ 上，此时三角尺旋转过的角度为．

(2)、继续将图2中的三角尺绕点 $O$ 按逆时针方向旋转至图3的位置，使得 $O N$ 在 $∠ A O C$ 的内部，试探究 $∠ A O M$ 与 $∠ N O C$ 之间满足什么等量关系？并说明理由．

查看试题解析