河北省沧州市2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. $\frac{1}{2020}$ 的倒数是（）

A、-2020 B、 $- \frac{1}{2020}$ C、 $\frac{1}{2020}$ D、2020

查看试题解析
2. 下列式子x，﹣3，- $\frac{1}{4} x^{2} + 2$ ，﹣mn中，单项式有（）个

A、1 B、2 C、3 D、4

查看试题解析
3. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数．如图，根据刘徽的这种表示法，观察图①，可推算图②中所得的数值为（）

A、﹣3 B、﹣2 C、﹣6 D、+6

查看试题解析
4. 2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为（）

A、 0.215×10⁸ B、2.15×10⁷ C、2.15×10⁶ D、21.5×10⁶

查看试题解析
5. 如图所示的是图纸上一个零件的标注，现有下列直径尺寸的产品（单位：mm），其中不合格的是（）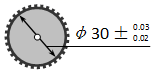

A、29.88mm B、30.03mm C、30.02mm D、29.98mm

查看试题解析
6. 如果单项式 $- x^{a + 1} y^{3}$ 与 $\frac{1}{2} y^{b} x^{2}$ 是同类项，那么 $a$ 、 $b$ 的值分别为（）

A、 $a = 2$ ， $b = 3$ B、 $a = 1$ ， $b = 2$ C、 $a = 1$ ， $b = 3$ D、 $a = 2$ ， $b = 2$

查看试题解析
7. 甲、乙两支同样的温度计如图所示放置，如果向左移动甲温度计，使其度数20正对着乙温度计的度数-10，那么此时甲温度计的度数-5正对着乙温度计的度数是（）

A、5 B、15 C、25 D、30

查看试题解析
8. 下列说法正确的是（）

A、单项式3ab的次数是1 B、3a－2a $^{2}$ b+2ab是三次三项式 C、单项式 $\frac{2 a b}{3}$ 的系数是2 D、－4a $^{2}$ b，3ab ， 5是多项式－4a $^{2}$ b+3ab-5的项

查看试题解析
9. 已知数a，b在数轴上表示的点的位置如图所示，则下列结论正确的是（　　）

A、a+b＞0 B、a﹣b＞0 C、﹣a＞﹣b＞a D、ab＞0

查看试题解析
10. 下列式子正确的是（）

A、 $x - (y - z) = x - y - z$ B、 $19 a^{2} b - 9 b a^{2} = 10 a^{2} b$ C、 $- 2 (x + y) - z = - 2 x + 2 y - z$ D、 $3 a^{3} + 2 a^{2} = 5 a^{5}$

查看试题解析
11. 如图，按图中的程序进行计算，如果输入的数是-2，那么输出的数是（）

A、-50 B、50 C、-250 D、250

查看试题解析
12. 如图，阴影部分是一个长方形截去两个四分之一的圆后剩余的部分，则它的面积是（其中 $a > 2 b$ ）（）

A、 $a b - \frac{π a^{2}}{4}$ B、 $a b - \frac{π b^{2}}{2}$ C、 $a b - \frac{π a^{2}}{2}$ D、 $a b - \frac{π b^{2}}{4}$

查看试题解析
13. 现定义一种新运算“※”，对任意有理数a、b，规定a※b=ab+a﹣b，例如：1※2=1×2+1﹣2=1，则2※（﹣3）等于（）

A、﹣3 B、﹣2 C、﹣1 D、0

查看试题解析
14. 如果 $a$ 和 $- 4 b$ 互为相反数，那么多项式 $2 (b - 2 a + 10) + 7 (a - 2 b - 3)$ 的值是（）

A、-3 B、-1 C、1 D、3

查看试题解析
15. 如图 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 分别是数轴上五个连续整数所对应的点，其中有一点是原点，数 $a$ 对应的点在 $B$ 与 $C$ 之间，数 $b$ 对应的点在 $D$ 与 $E$ 之间，若 $| a | + | b | = 3$ ，则原点可能是（）

A、点 $A$ B、点 $B$ 或点 $C$ C、点 $E$ D、点 $B$ 或点 $E$

查看试题解析
16. 将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形，…，如此下去，则第2020个图中共有正方形的个数为（）

A、2021 B、2020 C、6058 D、6061

查看试题解析

二、填空题

17. 向指定方向变化用正数表示，向指定方向的相反方向变化用负数表示，“体重减少 $1.5 kg$ ”换一种说法可以叙述为“体重增加 $kg$ ”.

查看试题解析
18. 若 $m$ 、 $n$ 满足 $| m + 3 | + {(n - 4)}^{2} = 0$ ，则 $m^{n} =$ ．

查看试题解析
19. 当k＝时，多项式 $x^{2} + (k - 1) x y - 3 y^{2} - 2 x y - 5$ 中不含xy项．

查看试题解析
20. 设[x]表示不超过x的整数中最大的整数，如：[1.99]=1，[﹣1.02]=﹣2，根据此规律计算：[﹣3.4]﹣[﹣0.6]=.

查看试题解析

三、解答题

21. 有理数： $\frac{1}{3}$ ，4，-1，-5，0， $3 \frac{1}{2}$ ，-2，1.

(1)、将上面各数在数轴上（图①）上表示出来，并把这些数用“ $<$ ”连接；

(2)、请将以上各数填到相应的集合的圈内（图②）.

查看试题解析
22.

(1)、计算： $6 \frac{3}{5} + 4 \frac{1}{7} + (- 5 \frac{3}{5}) - (- 6 \frac{6}{7})$ ；

(2)、计算： $- 2^{3} \times \frac{1}{6} + {(- 1)}^{2020} - (\frac{1}{5} - \frac{1}{3} + \frac{1}{6}) \times (- 30)$ ．

(3)、先化简，再求值： $2 (x - 2 y) - \frac{1}{3} (3 x - 6 y) + 2 x$ ，其中 $x = - 4$ ， $y = 3$ ．

查看试题解析
23. 2020年的“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩厂为满足市场需求计划每天生产5000个，由于各种原因实际每天生产量相比有出入，下表是二月份某一周的生产情况（超产为正，减产为负，单位：个）
星期
一
二
三
四
五
六
日
增减
+100
-200
+400
-100
-100
+350
+150

(1)、根据记录可知前三天共生产多少个口罩？

(2)、产量最多的一天比产量最少的一天多生产多少个？

(3)、该口罩加工厂实行计件工资制，每生产一个口罩0.2元，本周口罩加工厂应支付工人的工资总金额是多少元？

查看试题解析
24. 已知 $A = 3 a^{2} b - 2 a b^{2} + a b c$ ， $2 A + B = 4 a^{2} b - 3 a b^{2} + 4 a b c$ .

(1)、计算B的表达式；

(2)、求出 $2 A - B$ 的表达式；

(3)、小强同学说：“当 $c = - 2018$ 时和 $c = 2018$ 时，（2）中的结果都是一样的”，你认为你对吗？若 $a = \frac{1}{8}$ ， $b = \frac{1}{5}$ ，求（2）中式子的值.

查看试题解析
25. 甲、乙两家商场以同样的价格出售同样的电器，但各自推出的优惠方案不同，甲商场规定：凡超过 $1000$ 元的电器，超出的金额按 $80 %$ 收取；乙商场规定：凡超过 $800$ 元的电器，超出的金额按 $90 %$ 收取，某顾客购买的电器价格是 $x$ 元.

(1)、当 $x > 1000$ 时，分别用代数式表示在两家商场购买电器所需付的费用

(2)、当 $x = 1500$ 时，该顾客应选择哪一家商场购买比较合算？说明理由.

查看试题解析

星期	一	二	三	四	五	六	日
增减	+100	-200	+400	-100	-100	+350	+150