山西省孝义市2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. “保护生态，人人有责”．下列生态环保标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $(x - 2) (x + 3) = 0$ 的解是（）

A、 $x = 2$ B、 $x = - 3$ C、 $x_{1} = - 2, x_{2} = 3$ D、 $x_{1} = 2, x_{2} = - 3$

查看试题解析
3. 用配方法解方程 $x^{2} - 6 x - 8 = 0$ 时，配方结果正确的是（）

A、 ${(x - 3)}^{2} = 17$ B、 ${(x - 3)}^{2} = 14$ C、 ${(x - 6)}^{2} = 44$ D、 ${(x - 3)}^{2} = 1$

查看试题解析
4. 将抛物线y＝2x²平移，得到抛物线y＝2（x+4）²+1，下列平移正确的是（）

A、先向左平移4个单位，再向上平移1个单位 B、先向左平移4个单位，再向下平移1个单位 C、先向右平移4个单位，再向上平移1个单位 D、先向右平移4个单位，再向下平移1个单位

查看试题解析
5. 在某篮球邀请赛中，参赛的每两个队之间都要比赛一场，共比赛36场，设有x个队参赛，根据题意，可列方程为（）

A、 $\frac{1}{2} x (x - 1) = 36$ B、 $\frac{1}{2} x (x + 1) = 36$ C、 $x (x - 1) = 36$ D、 $x (x + 1) = 36$

查看试题解析
6. 已知点 $A (4, y_{1})$ ， $B (1, y_{2})$ ， $C (- 3, y_{3})$ 在函数 $y = - 3 {(x - 2)}^{2} + m$ （ $m$ 为常数）的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{2} > y_{1} > y_{3}$

查看试题解析
7. 利用图形的旋转可以设计出许多美丽的图案．如图2中的图案是由图1所示的基本图案以点 $O$ 为旋转中心，顺时针（或逆时针）旋转角度 $α$ ，依次旋转五次而组成，则旋转角 $α$ 的值不可能是（）

A、36° B、72° C、144° D、216°

查看试题解析
8. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列结论正确的是（）

A、 $a b c > 0$ B、 $2 a + b < 0$ C、关于 $x$ 的方程 $a x^{2} + b x + c + 3 = 0$ 有两个相等的实数根 D、 $9 a + 3 b + c < 0$

查看试题解析

9. 对于二次函数

y = x^{2} + b x + c

（

b

，

c

是常数）中自变量

x

与函数

y

的部分对应值如下表：

$x$	…	$- 1$	0	1	2	3	4	…
$y$	…	10	5	2	1	2	5	…

下列结论正确的是（）

A、函数图象开口向下 B、当

x = 5

时，

y = 10

C、当

x > 0

时，

y

随

x

的增大而增大 D、方程

x^{2} + b x + c = 0

有两个不相等的实数根

查看试题解析

10. 日历中含有丰富的数学知识，如在图1所示的日历中用阴影圈出9个数，这9个数的大小之间存在着某种规律.小慧在2020年某月的日历中也按图1所示方式圈出9个数（如图2），发现这9个数中最大的数与最小的数乘积是297，则这9个数中，中间的数

e

是（）

日	一	二	三	四	五	六
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

$a$	$b$	$c$
$d$	$e$	$f$
$g$	$h$	$i$

图1

图2

A、17 B、18 C、19 D、20

查看试题解析

二、填空题

11. 在平面直角坐标系中，已知点 $A (4, - 3)$ 与点 $B$ 关于原点对称，则点 $B$ 的坐标是．

查看试题解析
12. 已知关于 $x$ 的一元二次方程 $x^{2} - k x + k = 0$ 有两个相等的实数根，则 $k$ 的值是．

查看试题解析
13. “十三五”时期，我国新型城镇化建设坚持以人的城镇化为核心，更加注重提升人民群众的获得感和幸福感.2019年，我国城镇常住人口达到84843万人，常住人口城镇化率为超过60%．下图是2015年—2019年我国城镇常住人口统计图.若设2017年到2019年我国城镇常住人口的年平均增长率为 $x$ ，则可列方程．

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B A C = 30 °$ ， $A B = 4$ .将 $△ A B C$ 以点 $A$ 为中心，逆时针旋转60°，得到 $△ A B^{'} C^{'}$ ，连接 $B C^{'}$ ．则 $B C^{'} =$ ．

查看试题解析
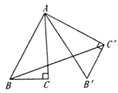15. “卢沟晓月”是著名的北京八景之一，每当黎明斜月西沉，月色倒影水中，更显明媚皎洁.古时乾隆皇帝曾在秋日路过卢沟桥，赋诗“半钩留照三秋淡，一练分波平镜明”于此，并题“卢沟晓月”，立碑于桥头.卢沟桥主桥拱可以近似看作抛物线，桥拱在水面的跨度 $O A$ 约为22米，若按如图所示方式建立平面直角坐标系，则主桥拱所在抛物线可以表示为 $y = - \frac{13}{121} {(x - 11)}^{2} + k$ ，则主桥拱最高点 $P$ 与其在水中倒影 $P^{'}$ 之间的距离为米．

查看试题解析

三、解答题

16.

(1)、求出抛物线 $y = - 3 x^{2} + 12 x - 9$ 与 $x$ 轴， $y$ 轴的交点坐标；

(2)、已知抛物线的顶点坐标为 $(2, - 4)$ ，且经过点 $(0, - 1)$ ，求出该抛物线的函数关系表达式．

查看试题解析
17. 如图， $⊙ O$ 中， $\overset{⌢}{A B} = \overset{⌢}{C D}$ ， $∠ A = ∠ C$ ， $A B$ 与 $C D$ 交于点 $P$ ．求证 $D P = B P$ ．

查看试题解析
18. 利用如图所示正方形网格，解决下列问题．

实践操作：

(1)、将 $△ A B C$ 以点 $O$ 为中心，顺时针旋转90°得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、作出 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{2} B_{2} C_{2}$ ．
观察发现：

(3)、 $△ A_{1} B_{1} C_{1}$ 经过一次图形变化就可以得到 $△ A_{2} B_{2} C_{2}$ ，这种图形变化是（填“平移”“旋转”或“轴对称”）．

查看试题解析
19. 阅读下列材料，完成相应任务：
我们已经学习过利用“配方法、公式法、因式分解法”解一元二次方程，对于关于 $x$ 的一元二次方程 $x^{2} + p x + q = 0$ ，还可以利用下面的方法求解．

将方程整理，得 $x (x + p) = - q$ .        ……………………第1步

变形得 $(x + \frac{p}{2} - \frac{p}{2}) (x + \frac{p}{2} + \frac{p}{2}) = - q$ .    ……………………第2步

得 ${(x + \frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} = - q$ .                ……………………第3步

于是得 ${(x + \frac{p}{2})}^{2} = {(\frac{p}{2})}^{2} - q$ ，即 ${(x + \frac{p}{2})}^{2} = \frac{p^{2} - 4 q}{4}$ .……第4步

当 $p^{2} - 4 q \geq 0$ 时，得 $x + \frac{p}{2} = \pm \frac{\sqrt{p^{2} - 4 q}}{2}$ .……………………第5步

得 $x_{1} = \frac{- p + \sqrt{p^{2} - 4 q}}{2}$ ， $x_{2} = \frac{- p - \sqrt{p^{2} - 4 q}}{2}$ .………………第6步

当 $p^{2} - 4 q < 0$ 时，该方程无实数解. ……………………………第7步

学习任务：

(1)、上述材料的第2步到第3步依据的一个数学公式是；以第4步到第5步将一元二次方程“降次”为两个一元一次方程，体现的数学思想主要是．

(2)、请用材料中提供的方法，解下列方程：
① $x^{2} + 10 x + 9 = 0$ ；② $2 x^{2} + 6 x - 3 = 0$ ．

查看试题解析
20. 图1所示是某广场地面示意图，该地面是由图2所示正方形地砖铺砌而成，某综合实践小组的同学测量图2所示地砖，得到 $A B = 100 c m$ ， $A E = A H = C F = C G$ ，且 $A E < B E$ ．于是他们抽象出如下两个数学问题：

(1)、问题（1）：若中间区域 $E F G H$ 的边 $E F = 2 E H$ ，求 $A E$ 的长度；

(2)、问题（2）：若中间区域 $E F G H$ 的面积为 $4800 c m^{2}$ ，求 $A E$ 的长度．
请你帮助他们解决上面的两个问题．

查看试题解析
21. 新冠疫情发生以来，中国蓬勃发展的消费市场、数字经济成为经济发展新的增长点，短视频和直播带货等新零售的快速崛起，让中国互联网经济持续火爆．吕梁某乡镇农贸公司以“吕梁有好礼，金秋消费季”为主题，开展直播带货活动，销售当地的一种特色农产品．公司在直播带货销售期间发现，该农产品每天的销售量 $y (k g)$ 与销售单价 $x$ （元 $/ k g$ ）之间近似满足一次函数关系，其函数图象如图所示：

(1)、求出 $y$ 与 $x$ 之间的函数关系式；

(2)、若该农产品的成本价为10元/千克，该农贸公司每天销售该特产的利润为 $W$ 元，求：当销售单价 $x$ 为多少元/千克时，每天的销售利润最大？最大利润为多少元？

查看试题解析
22. 综合与实践
问题情境

从“特殊到一般”是数学探究的常用方法之，类比特殊图形中的数量关系和探究方法可以发现一般图形具有的普遍规律．

如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $A D$ 为 $B C$ 边上的中线， $E$ 为 $A D$ 上一点，将 $△ A E C$ 以点 $C$ 为旋转中心，逆时针旋转90°得到 $△ B F C$ ， $A D$ 的延长线交线段 $B F$ 于点 $P$ ．探究线段 $E P$ ， $F P$ ， $B P$ 之间的数量关系．

(1)、数学思考
请你在图1中证明 $A P ⊥ B F$ ；

(2)、特例探究
如图2，当 $C E$ 垂直于 $A D$ 时，求证： $E P + F P = 2 B P$ ；

(3)、类比再探
请判断（2）的结论在图1中是否仍然成立？若成立，请证明；若不成立，请说明理由．

查看试题解析
23. 综合与探究
如图，抛物线 $y = \frac{4}{5} x^{2} + b x + c$ 经过点 $A (0 ， 4)$ ， $B (1 ， 0)$ ，与 $x$ 轴交于另一点 $C$ （点 $C$ 在点 $B$ 的右侧），点 $P (m ， n)$ 是第四象限内抛物线上的动点．

(1)、求抛物线的函数解析式及点 $C$ 的坐标；

(2)、若 $△ A P C$ 的面积为 $S$ ，请直接写出 $S$ 关于 $m$ 的函数关系表达式，并求出当 $m$ 的值为多少时， $S$ 的值最大？最大值为多少？

(3)、是否存在点 $P$ ，使得 $∠ P C O = ∠ A C B$ ？若存在，求出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析