山西省临汾市襄汾县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式是最简二次根式的是（）

A、 $\sqrt{13}$ B、 $\sqrt{12}$ C、 $\sqrt{a^{2}}$ D、 $\sqrt{\frac{5}{3}}$

查看试题解析
2. 下列运算，结果正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $3 + \sqrt{2} = 3 \sqrt{2}$ C、 $\sqrt{6} \div \sqrt{2} = 3$ D、 $\sqrt{6} \times \sqrt{2} = 2 \sqrt{3}$

查看试题解析
3. 关于 $x$ 的一元二次方程 $a x^{2} - 2 x + 2 = 0$ 有两个相等的实数根，则 $a$ 的值为（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、1 D、1

查看试题解析
4. 如图，面积为1的等边三角形 $A B C$ 中， $D ， E ， F$ 分别是 $A B$ ， $B C$ ， $C A$ 的中点，则 $Δ D E F$ 的面积是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
5. 如图，在 $4 \times 5$ 的正方形网格中，每个小正方形的边长都是1， $△ A B C$ 的顶点都在这些小正方形的顶点上，那么 $\sin ∠ A C B$ 的值为（）．

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{\sqrt{17}}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 下列说法错误的是（）

A、含 $30^{\circ}$ 角的直角三角形与含 $60^{\circ}$ 角的直角三角形是相似的 B、所有的矩形是相似的 C、所有边数相等的正多边形是相似的 D、所有的等边三角形都是相似的

查看试题解析
7. 如图，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60米到达C点，测得点B在点C的北偏东60°方向，则这段河的宽度为（）

A、60( $\sqrt{3}$ +1)米 B、30( $\sqrt{3}$ +1)米 C、(90﹣30 $\sqrt{3}$ )米 D、30( $\sqrt{3}$ ﹣1)米

查看试题解析
8. 如图，已知 $A B / / C D / / E F$ ，它们依次交直线 $l_{1}$ 、 $l_{2}$ 于点 $A$ 、 $D$ 、 $F$ 和点 $B$ 、 $C$ 、 $E$ ，如果 $A D ： D F = 3 ： 1$ ， $B E = 10$ ，那么 $C E$ 等于（）

A、 $\frac{10}{3}$ B、 $\frac{20}{3}$ C、 $\frac{5}{2}$ D、 $\frac{15}{2}$

查看试题解析
9. 国家统计局统计数据显示，我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为（）

A、 $5000 (1 + 2 x) = 7500$ B、 $5000 \times 2 (1 + x) = 7500$ C、 $5000 {(1 + x)}^{2} = 7500$ D、 $5000 + 5000 (1 + x) + 5000 {(1 + x)}^{2} = 7500$

查看试题解析
10. 在△ABC中，∠ACB＝90°，用直尺和圆规在AB上确定点D，使△ACD∽△CBD，根据作图痕迹判断，正确的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 已知 $y = \sqrt{x - 2} - \sqrt{2 - x} + 3$ ，求 $y^{x} =$ ．

查看试题解析
12. 若两个相似五边形的相似比为 3:5，则它们的面积比为

查看试题解析
13. 已知关于x的一元二次方程 $(a - 1) x^{2} - 2 x + a^{2} - 1 = 0$ 有一个根为 $x = 0$ ，则a的值为．

查看试题解析
14. 如图，△ABC与△A′B′C′是位似图形，且顶点都在格点上，则位似中心的坐标是.

查看试题解析
15. 如图，已知四边形ABCD ， AC与BD相交于点O ， ∠ABC=∠DAC=90°， $\tan ∠ A C B = \frac{1}{2} ， \frac{B O}{O D} = \frac{4}{3}$ ，则 $\frac{S_{△ A B D}}{S_{△ C B D}}$ = ．

查看试题解析

三、解答题

16. 计算：

(1)、 ${(\frac{1}{2})}^{- 2} - | \sqrt{2} - 3 | + 2 t a n 45 ° - {(2020 - π)}^{0}$

(2)、 $(\sqrt{2} + 1) (\sqrt{2} - 1) + {(\sqrt{3} - 2)}^{2}$

查看试题解析
17. 按要求解方程

(1)、 $x^{2} - 3 x + 1 = 0$ （公式法)

(2)、 ${(x + 1)}^{2} = 2 x + 2$ （因式分解法）

(3)、 $x^{2} + 2 x - 399 = 0$ （配方法）

查看试题解析
18.
已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

(1)、画出△ABC向下平移4个单位长度得到的△A₁B₁C₁ ，点C₁的坐标是；

(2)、以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是；

(3)、△A₂B₂C₂的面积是平方单位．

查看试题解析
19. 某商场将进货价为30元的台灯以40元售出，平均每月能售出600个，调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个．为了实现平均每月10000元的销售利润，商场决定采取调控价格的措施，扩大销售量，减少库存，这种台灯的售价应定为多少元?这时应进台灯多少个?

查看试题解析
20. 有一个坡度i=1：2的斜坡AB，顶部A处的高AC为4米，B、C在同一水平地面上，其横截面如图。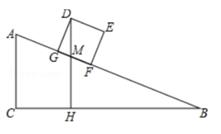

(1)、求该斜坡的坡面AB的长度。

(2)、现有一个侧面图为矩形DEFG的长方体货柜，其中DE=2.5米，EF=2米，该货柜沿斜坡向下时，点D离BC所在水平面的高度不断变化，求当BF=3.5米时，点D离BC所在水平面的高度DH。

查看试题解析
21. 求代数式 $a + \sqrt{1 - 2 a + a^{2}}$ 的值，其中 $a = 1007$ ．
如图是小亮和小芳的解答过程：

(1)、的解法是错误的；

(2)、错误的原因在于未能正确的运用二次根式的性质：；

(3)、求代数式 $a + 2 \sqrt{a^{2} - 6 a + 9}$ 的值，其中 $a = - 2020$

查看试题解析
22. 阅读材料：为解方程 ${(x^{2} - 1)}^{2} - 3 (x^{2} - 1) = 0$ ，我们可以将 $x^{2} - 1$ 视为一个整体，然后设 $x^{2} - 1 = y ，$ 将原方程化为 $y^{2} - 3 y = 0$ ①，解得 $y_{1} = 0 ， y_{2} = 3$ ．
当 $y = 0$ 时 $x^{2} - 1 = 0 ，$ $∴ x^{2} = 1 ，$ $∴ x = \pm 1$

当 $y = 3$ 时， $x^{2} - 1 = 3$ ， $∴ x^{2} = 4 ， ∴ x = \pm 2$

$∴$ 原方程的解为 $x_{1} = 1 ， x_{2} = - 1 ， x_{3} = 2 ， x_{4} = 2$

阅读后解答问题：

(1)、在由原方程得到方程①的过程中，利用法达到了降次的目的，体现了的数学思想；

(2)、利用上述材料中的方法解方程： ${(x^{2} + x)}^{2} - (x^{2} + x) - 2 = 0$

查看试题解析
23. 已知：如图，在△ABC中，点D、E分别在边BC、AC上，点F在DE的延长线上，AD＝AF，AE•CE＝DE•EF．

(1)、求证：△ADE∽△ACD；

(2)、如果AE•BD＝EF•AF，求证：AB＝AC．

查看试题解析